Question Number 169436 by mathocean1 last updated on 30/Apr/22
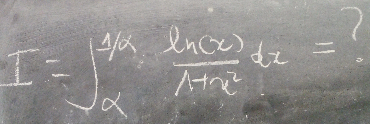
Commented by mathocean1 last updated on 30/Apr/22

$${with}\:\mathrm{0}<\alpha<\mathrm{1} \\ $$
Answered by Mathspace last updated on 01/May/22
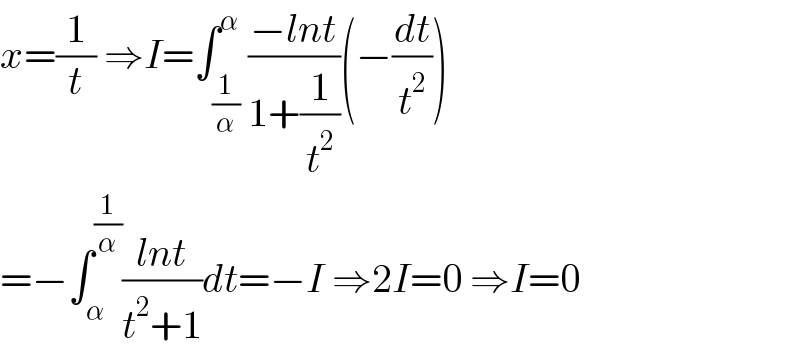
$${x}=\frac{\mathrm{1}}{{t}}\:\Rightarrow{I}=\int_{\frac{\mathrm{1}}{\alpha}} ^{\alpha} \frac{−{lnt}}{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}\left(−\frac{{dt}}{{t}^{\mathrm{2}} }\right) \\ $$$$=−\int_{\alpha} ^{\frac{\mathrm{1}}{\alpha}} \frac{{lnt}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}=−{I}\:\Rightarrow\mathrm{2}{I}=\mathrm{0}\:\Rightarrow{I}=\mathrm{0} \\ $$
