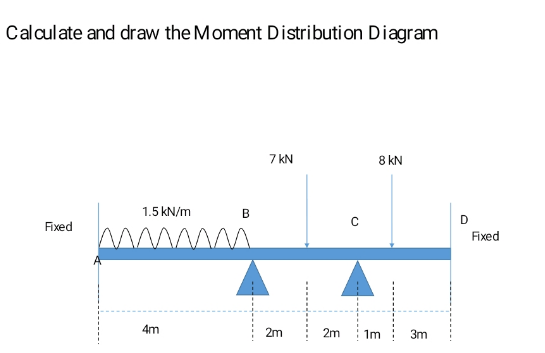
Question Number 169448 by BHOOPENDRA last updated on 30/Apr/22
Commented by BHOOPENDRA last updated on 30/Apr/22

$${calculation}\:{sir} \\ $$
Commented by BHOOPENDRA last updated on 30/Apr/22

$${thankyou}\:{sir} \\ $$
Commented by BHOOPENDRA last updated on 01/May/22

Commented by BHOOPENDRA last updated on 01/May/22

Commented by BHOOPENDRA last updated on 01/May/22

$${sir}\:{please}\:{help}\:{me}\:{where}\:{i}\:{m}\:{doing}\: \\ $$$${wrong}\:{can}\:{you}\:{please}\:{help}\:{me}\:{in}\:{the} \\ $$$${solution} \\ $$
Commented by mr W last updated on 01/May/22
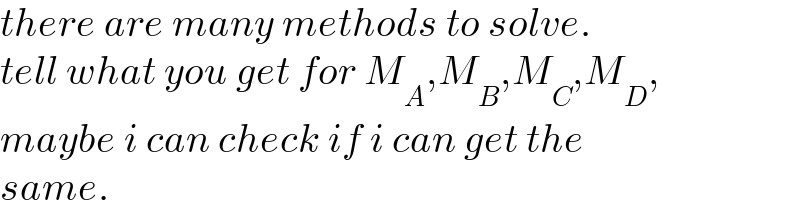
$${there}\:{are}\:{many}\:{methods}\:{to}\:{solve}. \\ $$$${tell}\:{what}\:{you}\:{get}\:{for}\:{M}_{{A}} ,{M}_{{B}} ,{M}_{{C}} ,{M}_{{D}} , \\ $$$${maybe}\:{i}\:{can}\:{check}\:{if}\:{i}\:{can}\:{get}\:{the} \\ $$$${same}. \\ $$
Commented by BHOOPENDRA last updated on 01/May/22
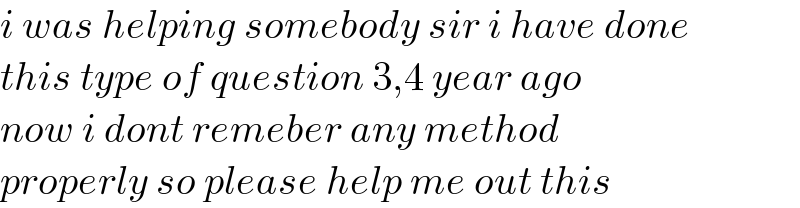
$${i}\:{was}\:{helping}\:{somebody}\:{sir}\:{i}\:{have}\:{done} \\ $$$${this}\:{type}\:{of}\:{question}\:\mathrm{3},\mathrm{4}\:{year}\:{ago} \\ $$$${now}\:{i}\:{dont}\:{remeber}\:{any}\:{method} \\ $$$${properly}\:{so}\:{please}\:{help}\:{me}\:{out}\:{this} \\ $$
Commented by mr W last updated on 01/May/22

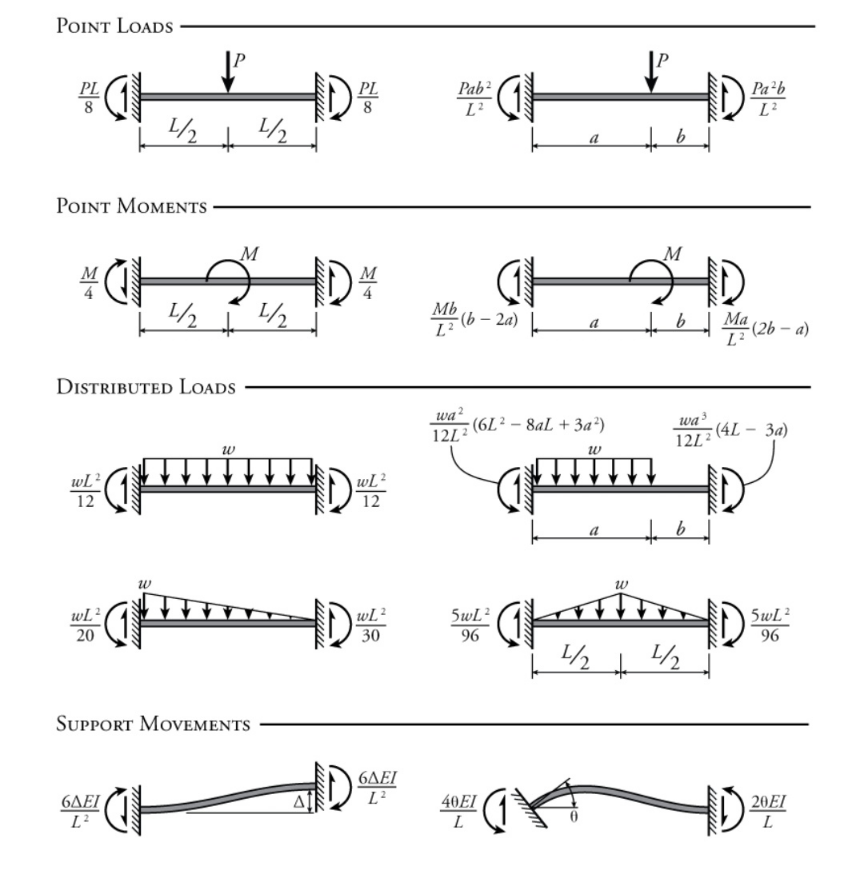
$${For}\:{calculation}\:{by}\:{hand}\:{we}\:{apply} \\ $$$${usually} \\ $$$${Method}\:{I}:\: \\ $$$${we}\:{take}\:{the}\:{moments}\:{at}\:{the}\:{supports} \\ $$$${as}\:{unknowns} \\ $$$$\Rightarrow{system}\:{with}\:\mathrm{4}\:{unknowns} \\ $$$${Method}\:{II}: \\ $$$${we}\:{take}\:{the}\:{slopes}\:{at}\:{the}\:{supports}\:{B},{C} \\ $$$${as}\:{unknowns} \\ $$$$\Rightarrow{system}\:{with}\:\mathrm{2}\:{unknowns} \\ $$$$ \\ $$$${both}\:{are}\:{easy},\:{but}\:{it}\:{needs}\:{time}\:{to} \\ $$$${work}\:{out}… \\ $$
Commented by BHOOPENDRA last updated on 01/May/22

$${thankyou}\:{sir}\:{i}\:{did}\:{roughly}\:{but}\:{i}\:{did}\:{not}\:{get} \\ $$$${the}\:{ans}.{so}\:{can}\:{you}\:{please}\:{calculate}\:{it} \\ $$$${sir} \\ $$
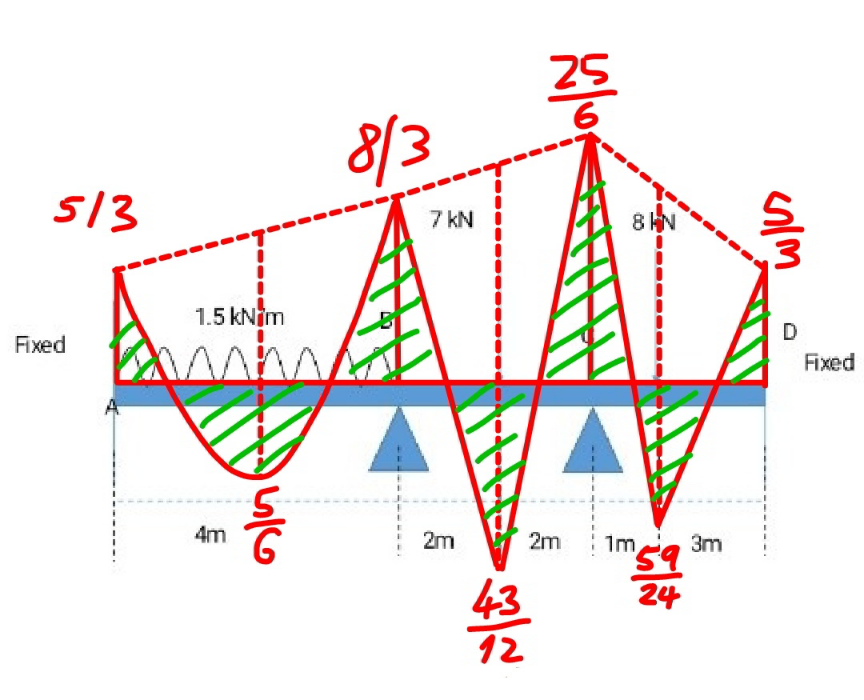
Answered by mr W last updated on 01/May/22

$$\boldsymbol{{Moment}}\:\boldsymbol{{under}}\:\boldsymbol{{loads}}: \\ $$$${M}_{{A},{r},\mathrm{0}} =−\frac{\mathrm{1}.\mathrm{5}×\mathrm{4}^{\mathrm{2}} }{\mathrm{12}}=−\mathrm{2}\:{KNm} \\ $$$${M}_{{B},{l},\mathrm{0}} =\frac{\mathrm{1}.\mathrm{5}×\mathrm{4}^{\mathrm{2}} }{\mathrm{12}}=\mathrm{2}\:{KNm} \\ $$$${M}_{{B},{r},\mathrm{0}} =−\frac{\mathrm{7}×\mathrm{4}}{\mathrm{8}}=−\mathrm{3}.\mathrm{5}\:{KNm} \\ $$$${M}_{{C},{l},\mathrm{0}} =\frac{\mathrm{7}×\mathrm{4}}{\mathrm{8}}=\mathrm{3}.\mathrm{5}\:{KNm} \\ $$$${M}_{{C},{r},\mathrm{0}} =−\frac{\mathrm{8}×\mathrm{1}×\mathrm{3}^{\mathrm{2}} }{\mathrm{4}^{\mathrm{2}} }=−\mathrm{4}.\mathrm{5}\:{KNm} \\ $$$${M}_{{D},{l},\mathrm{0}} =\frac{\mathrm{8}×\mathrm{3}×\mathrm{1}^{\mathrm{2}} }{\mathrm{4}^{\mathrm{2}} }=\mathrm{1}.\mathrm{5}\:{KNm} \\ $$$$ \\ $$$$\boldsymbol{{Moment}}\:\boldsymbol{{under}}\:\boldsymbol{\theta}_{\mathrm{1}} =\boldsymbol{{slope}}\:\boldsymbol{{at}}\:\boldsymbol{{B}}×\boldsymbol{{EI}}=\mathrm{1}: \\ $$$${M}_{{A},{r},\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{4}}=\mathrm{0}.\mathrm{5}\:{KNm} \\ $$$${M}_{{B},{l},\mathrm{1}} =\frac{\mathrm{4}}{\mathrm{4}}=\mathrm{1}\:{KNm} \\ $$$${M}_{{B},{r},\mathrm{1}} =\frac{\mathrm{4}}{\mathrm{4}}=\mathrm{1}\:{KNm} \\ $$$${M}_{{C},{l},\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{4}}=\mathrm{0}.\mathrm{5}\:{KNm} \\ $$$${M}_{{C},{r},\mathrm{1}} =\mathrm{0}\:{KNm} \\ $$$${M}_{{D},{l},\mathrm{1}} =\mathrm{0}\:{KNm} \\ $$$$ \\ $$$$\boldsymbol{{Moment}}\:\boldsymbol{{under}}\:\boldsymbol{\theta}_{\mathrm{2}} =\boldsymbol{{slope}}\:\boldsymbol{{at}}\:\boldsymbol{{C}}×\boldsymbol{{EI}}=\mathrm{1}: \\ $$$${M}_{{A},{r},\mathrm{2}} =\mathrm{0}\:{KNm} \\ $$$${M}_{{B},{l},\mathrm{2}} =\mathrm{0}{Nm} \\ $$$${M}_{{B},{r},\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{4}}=\mathrm{0}.\mathrm{5}\:{KNm} \\ $$$${M}_{{C},{l},\mathrm{2}} =\frac{\mathrm{4}}{\mathrm{4}}=\mathrm{1}\:{KNm} \\ $$$${M}_{{C},{r},\mathrm{2}} =\frac{\mathrm{4}}{\mathrm{4}}=\mathrm{1}\:{KNm} \\ $$$${M}_{{D},{l},\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{4}}=\mathrm{0}.\mathrm{5}\:{KNm} \\ $$$$ \\ $$$$\Sigma{M}_{{B}} =\left(\mathrm{1}+\mathrm{1}\right)\theta_{\mathrm{1}} +\mathrm{0}.\mathrm{5}\theta_{\mathrm{2}} +\mathrm{2}−\mathrm{3}.\mathrm{5}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}\theta_{\mathrm{1}} +\theta_{\mathrm{2}} =\mathrm{3}\:\:\:…\left({i}\right) \\ $$$$\Sigma{M}_{{C}} =\mathrm{0}.\mathrm{5}\theta_{\mathrm{1}} +\left(\mathrm{1}+\mathrm{1}\right)\theta_{\mathrm{2}} +\mathrm{3}.\mathrm{5}−\mathrm{4}.\mathrm{5}=\mathrm{0} \\ $$$$\Rightarrow\theta_{\mathrm{1}} +\mathrm{4}\theta_{\mathrm{2}} =\mathrm{2}\:\:\:…\left({ii}\right) \\ $$$${solving}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{we}\:{get} \\ $$$$\theta_{\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\theta_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$ \\ $$$${M}_{{A},{r}} =−\mathrm{2}+\mathrm{0}.\mathrm{5}×\left(\frac{\mathrm{2}}{\mathrm{3}}\right)=−\frac{\mathrm{5}}{\mathrm{3}}\:{KNm} \\ $$$${M}_{{B},{l}} =\mathrm{2}+\mathrm{1}×\left(\frac{\mathrm{2}}{\mathrm{3}}\right)+\mathrm{0}×\left(\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{8}}{\mathrm{3}}\:{KNm} \\ $$$${M}_{{B},{r}} =−\mathrm{3}.\mathrm{5}+\mathrm{1}×\left(\frac{\mathrm{2}}{\mathrm{3}}\right)+\mathrm{0}.\mathrm{5}×\left(\frac{\mathrm{1}}{\mathrm{3}}\right)=−\frac{\mathrm{8}}{\mathrm{3}}\:{KNm} \\ $$$${M}_{{C},{l}} =\mathrm{3}.\mathrm{5}+\mathrm{0}.\mathrm{5}×\left(\frac{\mathrm{2}}{\mathrm{3}}\right)+\mathrm{1}×\left(\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{25}}{\mathrm{6}}\:{KNm} \\ $$$${M}_{{C},{r}} =−\mathrm{4}.\mathrm{5}+\mathrm{0}×\left(\frac{\mathrm{2}}{\mathrm{3}}\right)+\mathrm{1}×\left(\frac{\mathrm{1}}{\mathrm{3}}\right)=−\frac{\mathrm{25}}{\mathrm{6}}\:{KNm} \\ $$$${M}_{{D},{l}} =\mathrm{1}.\mathrm{5}+\mathrm{0}×\left(\frac{\mathrm{2}}{\mathrm{3}}\right)+\mathrm{0}.\mathrm{5}×\left(\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{5}}{\mathrm{3}}\:{KNm} \\ $$
Commented by BHOOPENDRA last updated on 01/May/22

$${thankyou}\:{sir} \\ $$
Commented by mr W last updated on 01/May/22
Commented by mr W last updated on 01/May/22