Menu Close

Question-169458

Tinku Tara 0 Comments
Pin




Question Number 169458 by ajfour last updated on 30/Apr/22
Commented by ajfour last updated on 30/Apr/22
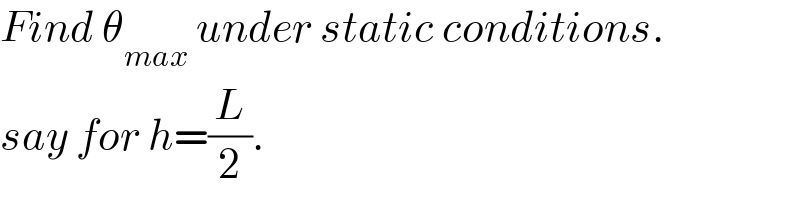
Find θ_(max) under static conditions. say for h=(L/2).
$${Find}\:\theta_{{max}} \:{under}\:{static}\:{conditions}. \\ $$$${say}\:{for}\:{h}=\frac{{L}}{\mathrm{2}}. \\ $$
Answered by mr W last updated on 01/May/22
Commented by mr W last updated on 04/May/22
C=common center of gravity from M and m AC×(m+M)=m×L+M×(L/2) ⇒AC=(((2m+M)L)/(2(m+M)))=b, say AB=(h/(sin θ)) tan φ=μ SC=((BC)/(sin θ))=((AB−AC)/(sin θ))=(((h/(sin θ))−b)/(sin θ)) ((AC)/(sin φ))=((SC)/(sin ((π/2)−φ−θ)))=((SC)/(cos (θ+φ))) (b/(sin φ))=(((h/(sin θ))−b)/(sin θ cos (θ+φ))) (1/(sin φ))=(((h/(b sin θ))−1)/(sin θ cos (θ+φ))) let λ=(h/b)=((2(m+M)h)/((2m+M)L)) (1/(sin φ))=((λ−sin θ)/(sin^2 θ cos (θ+φ))) (1/(sin φ))=((λ−sin θ)/(sin^2 θ (cos θ cos φ−sin θ sin φ))) ⇒sin^2 θ (((cos θ)/μ)−sin θ)+sin θ=λ example: m=(M/2), h=(L/2), μ=0.5 λ=((2(0.5+1)×0.5)/((2×0.5+1)))=(3/4) sin^2 θ (2 cos θ−sin θ)+sin θ=(3/4) ⇒θ_1 ≈27.8087° and θ_2 ≈68.8197°
$${C}={common}\:{center}\:{of}\:{gravity}\:{from} \\ $$$$\:\:\:\:\:\:\:{M}\:{and}\:{m} \\ $$$${AC}×\left({m}+{M}\right)={m}×{L}+{M}×\frac{{L}}{\mathrm{2}} \\ $$$$\Rightarrow{AC}=\frac{\left(\mathrm{2}{m}+{M}\right){L}}{\mathrm{2}\left({m}+{M}\right)}={b},\:{say} \\ $$$${AB}=\frac{{h}}{\mathrm{sin}\:\theta} \\ $$$$\mathrm{tan}\:\phi=\mu \\ $$$${SC}=\frac{{BC}}{\mathrm{sin}\:\theta}=\frac{{AB}−{AC}}{\mathrm{sin}\:\theta}=\frac{\frac{{h}}{\mathrm{sin}\:\theta}−{b}}{\mathrm{sin}\:\theta} \\ $$$$\frac{{AC}}{\mathrm{sin}\:\phi}=\frac{{SC}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\phi−\theta\right)}=\frac{{SC}}{\mathrm{cos}\:\left(\theta+\phi\right)} \\ $$$$\frac{{b}}{\mathrm{sin}\:\phi}=\frac{\frac{{h}}{\mathrm{sin}\:\theta}−{b}}{\mathrm{sin}\:\theta\:\mathrm{cos}\:\left(\theta+\phi\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}\:\phi}=\frac{\frac{{h}}{{b}\:\mathrm{sin}\:\theta}−\mathrm{1}}{\mathrm{sin}\:\theta\:\mathrm{cos}\:\left(\theta+\phi\right)} \\ $$$${let}\:\lambda=\frac{{h}}{{b}}=\frac{\mathrm{2}\left({m}+{M}\right){h}}{\left(\mathrm{2}{m}+{M}\right){L}} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}\:\phi}=\frac{\lambda−\mathrm{sin}\:\theta}{\mathrm{sin}^{\mathrm{2}} \:\theta\:\mathrm{cos}\:\left(\theta+\phi\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin}\:\phi}=\frac{\lambda−\mathrm{sin}\:\theta}{\mathrm{sin}^{\mathrm{2}} \:\theta\:\left(\mathrm{cos}\:\theta\:\mathrm{cos}\:\phi−\mathrm{sin}\:\theta\:\mathrm{sin}\:\phi\right)} \\ $$$$\Rightarrow\mathrm{sin}^{\mathrm{2}} \:\theta\:\left(\frac{\mathrm{cos}\:\theta}{\mu}−\mathrm{sin}\:\theta\right)+\mathrm{sin}\:\theta=\lambda \\ $$$${example}: \\ $$$${m}=\frac{{M}}{\mathrm{2}},\:{h}=\frac{{L}}{\mathrm{2}},\:\mu=\mathrm{0}.\mathrm{5} \\ $$$$\lambda=\frac{\mathrm{2}\left(\mathrm{0}.\mathrm{5}+\mathrm{1}\right)×\mathrm{0}.\mathrm{5}}{\left(\mathrm{2}×\mathrm{0}.\mathrm{5}+\mathrm{1}\right)}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\theta\:\left(\mathrm{2}\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)+\mathrm{sin}\:\theta=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\theta_{\mathrm{1}} \approx\mathrm{27}.\mathrm{8087}°\:{and}\:\theta_{\mathrm{2}} \approx\mathrm{68}.\mathrm{8197}° \\ $$
Commented by BHOOPENDRA last updated on 01/May/22
great sir
$${great}\:{sir} \\ $$
Commented by ajfour last updated on 04/May/22
great way sir.
$${great}\:{way}\:{sir}. \\ $$
Commented by mr W last updated on 04/May/22
following diagram shows the two states. equilibrium is if θ≤θ_1 or θ≥θ_2 .
$${following}\:{diagram}\:{shows}\:{the}\:{two} \\ $$$${states}.\:{equilibrium}\:{is}\:{if}\:\theta\leqslant\theta_{\mathrm{1}} \:{or} \\ $$$$\theta\geqslant\theta_{\mathrm{2}} . \\ $$
Commented by mr W last updated on 04/May/22
Answered by ajfour last updated on 02/May/22
Commented by mr W last updated on 03/May/22
very nice sir!
$${very}\:{nice}\:{sir}! \\ $$
Commented by ajfour last updated on 03/May/22
Mg((L/2)cos θ)+mgLcos θ =((Fh)/(sin θ)) N=(M+m)g−Fcos θ μN=Fsin θ ⇒ F(sin θ+μcos θ)=μ(M+m)g ⇒ Mg((L/2)cos θ)+mgLcos θ =((μgh(M+m))/(sin θ(sin θ+μcos θ))) say (m/M)=λ , h=βL ⇒ ((cos θ)/2)+λcos θ=((μβ(λ+1))/(sin θ(sin θ+μcos θ))) ⇒ (sin θ+μcos θ)sin θcos θ(λ+(1/2)) =βμ(λ+1) for μ=λ=β=(1/2) (2sin θ+cos θ)sin θcos θ=(3/4) 16(2t+1)^2 t^2 =9(1+t^2 )^3 t≈ 0.5274, 2.5808 θ=tan^(−1) t ≈ 27.807° , 68.819°
$${Mg}\left(\frac{{L}}{\mathrm{2}}\mathrm{cos}\:\theta\right)+{mgL}\mathrm{cos}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{Fh}}{\mathrm{sin}\:\theta} \\ $$$${N}=\left({M}+{m}\right){g}−{F}\mathrm{cos}\:\theta \\ $$$$\mu{N}={F}\mathrm{sin}\:\theta\:\:\:\: \\ $$$$\Rightarrow \\ $$$$\:{F}\left(\mathrm{sin}\:\theta+\mu\mathrm{cos}\:\theta\right)=\mu\left({M}+{m}\right){g} \\ $$$$\Rightarrow \\ $$$${Mg}\left(\frac{{L}}{\mathrm{2}}\mathrm{cos}\:\theta\right)+{mgL}\mathrm{cos}\:\theta \\ $$$$\:\:=\frac{\mu{gh}\left({M}+{m}\right)}{\mathrm{sin}\:\theta\left(\mathrm{sin}\:\theta+\mu\mathrm{cos}\:\theta\right)} \\ $$$${say}\:\:\frac{{m}}{{M}}=\lambda\:\:,\:\:{h}=\beta{L}\:\:\:\Rightarrow \\ $$$$\frac{\mathrm{cos}\:\theta}{\mathrm{2}}+\lambda\mathrm{cos}\:\theta=\frac{\mu\beta\left(\lambda+\mathrm{1}\right)}{\mathrm{sin}\:\theta\left(\mathrm{sin}\:\theta+\mu\mathrm{cos}\:\theta\right)} \\ $$$$\Rightarrow \\ $$$$\:\left(\mathrm{sin}\:\theta+\mu\mathrm{cos}\:\theta\right)\mathrm{sin}\:\theta\mathrm{cos}\:\theta\left(\lambda+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:=\beta\mu\left(\lambda+\mathrm{1}\right) \\ $$$$\:\:\:\:{for}\:\:\:\mu=\lambda=\beta=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\mathrm{2sin}\:\theta+\mathrm{cos}\:\theta\right)\mathrm{sin}\:\theta\mathrm{cos}\:\theta=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{16}\left(\mathrm{2}{t}+\mathrm{1}\right)^{\mathrm{2}} {t}^{\mathrm{2}} =\mathrm{9}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{3}} \\ $$$${t}\approx\:\:\mathrm{0}.\mathrm{5274},\:\:\mathrm{2}.\mathrm{5808} \\ $$$$\theta=\mathrm{tan}^{−\mathrm{1}} {t}\:\:\:\approx\:\mathrm{27}.\mathrm{807}°\:,\:\mathrm{68}.\mathrm{819}° \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *