Question Number 169466 by BHOOPENDRA last updated on 30/Apr/22

Answered by mr W last updated on 01/May/22

$${deflection}\:{at}\:{center}\:{of}\:{simple}\:{beam}\: \\ $$$${under}\:{uniform}\:{load}\:{is} \\ $$$$\delta=\frac{\mathrm{5}{wl}^{\mathrm{4}} }{\mathrm{384}{EI}} \\ $$$$\Rightarrow{EI}=\frac{\mathrm{5}{wl}^{\mathrm{4}} }{\mathrm{384}\delta} \\ $$$${with}\:{w}=\mathrm{30}\:{KN}/{m},\:{l}=\mathrm{4}{m},\:\delta=\mathrm{0}.\mathrm{015}{m} \\ $$$$ \\ $$$${crippling}\:{load}\:{of}\:{the}\:{same}\:{beam}\: \\ $$$${when}\:{used}\:{as}\:{column} \\ $$$$\left({i}\right)\:{Euler}\:{case}\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\:{P}=\frac{\pi^{\mathrm{2}} {EI}}{{l}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{{l}^{\mathrm{2}} }×\frac{\mathrm{5}{wl}^{\mathrm{4}} }{\mathrm{384}\delta}=\frac{\mathrm{5}\pi^{\mathrm{2}} {wl}^{\mathrm{2}} }{\mathrm{384}\delta} \\ $$$$\:\:\:\:\:\:\:\:\:\:\approx\mathrm{4}\:\mathrm{112}\:{KN} \\ $$$$\left({ii}\right)\:{Euler}\:{case}\:\mathrm{3} \\ $$$$\:\:\:\:\:\:\:{P}=\frac{\mathrm{2}\pi^{\mathrm{2}} {EI}}{{l}^{\mathrm{2}} }=\frac{\mathrm{2}\pi^{\mathrm{2}} }{{l}^{\mathrm{2}} }×\frac{\mathrm{5}{wl}^{\mathrm{4}} }{\mathrm{384}\delta}=\frac{\mathrm{10}\pi^{\mathrm{2}} {wl}^{\mathrm{2}} }{\mathrm{384}\delta} \\ $$$$\:\:\:\:\:\:\:\:\:\:\approx\mathrm{8}\:\mathrm{225}\:{KN} \\ $$$$\left({iii}\right)\:{Euler}\:{case}\:\mathrm{2} \\ $$$$\:\:\:\:\:\:\:{P}=\frac{\mathrm{4}\pi^{\mathrm{2}} {EI}}{{l}^{\mathrm{2}} }=\frac{\mathrm{4}\pi^{\mathrm{2}} }{{l}^{\mathrm{2}} }×\frac{\mathrm{5}{wl}^{\mathrm{4}} }{\mathrm{384}\delta}=\frac{\mathrm{20}\pi^{\mathrm{2}} {wl}^{\mathrm{2}} }{\mathrm{384}\delta} \\ $$$$\:\:\:\:\:\:\:\:\:\:\approx\mathrm{16}\:\mathrm{449}\:{KN} \\ $$
Commented by mr W last updated on 01/May/22

Commented by mr W last updated on 01/May/22

Commented by BHOOPENDRA last updated on 01/May/22

Commented by BHOOPENDRA last updated on 01/May/22
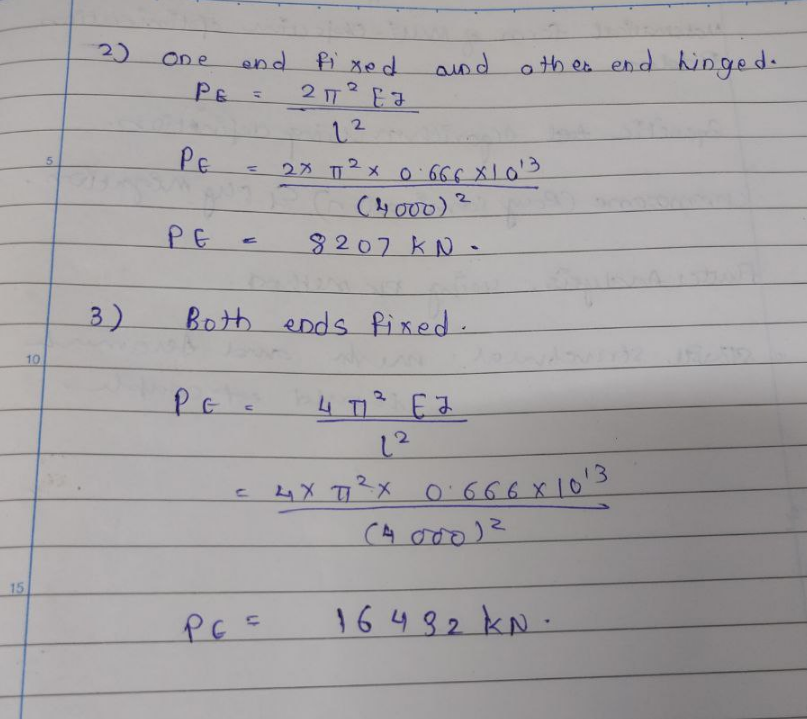
Commented by BHOOPENDRA last updated on 01/May/22
$${Got}\:{the}\:{same}\:{thankyou}\:{sir} \\ $$
Commented by kapoorshah last updated on 01/May/22
$${Mr}\:{W} \\ $$$${Are}\:{you}\:{a}\:{civil}\:{engineer}? \\ $$
