Question Number 169498 by bagjagugum123 last updated on 01/May/22
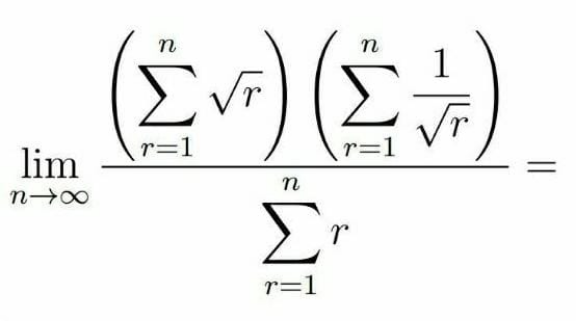
Commented by infinityaction last updated on 01/May/22

$$\frac{\mathrm{8}}{\mathrm{3}} \\ $$
Commented by bagjagugum123 last updated on 01/May/22

$${how}\:{solutions}? \\ $$
Commented by infinityaction last updated on 01/May/22

$$\:\:\:\:\:\:\:\left(\boldsymbol{\mathrm{let}}\right)\:\boldsymbol{\mathrm{p}}\:\:=\:\:\:\underset{{n}\rightarrow\infty} {\boldsymbol{\mathrm{lim}}}\:\frac{\sqrt{\boldsymbol{\mathrm{n}}\:}\underset{\boldsymbol{\mathrm{r}}=\mathrm{1}} {\overset{\boldsymbol{\mathrm{n}}} {\boldsymbol{\sum}}}\sqrt{\frac{\boldsymbol{\mathrm{r}}}{\boldsymbol{\mathrm{n}}}}\:\:×\:\frac{\mathrm{1}}{\:\sqrt{\boldsymbol{\mathrm{n}}}}\:\underset{\boldsymbol{\mathrm{r}}=\mathrm{1}} {\overset{\boldsymbol{\mathrm{n}}} {\boldsymbol{\sum}}}\sqrt{\frac{\boldsymbol{\mathrm{n}}}{\boldsymbol{\mathrm{r}}}}}{\boldsymbol{\mathrm{n}}\underset{\boldsymbol{\mathrm{r}}=\mathrm{1}} {\overset{\boldsymbol{\mathrm{n}}} {\boldsymbol{\sum}}}\frac{\boldsymbol{\mathrm{r}}}{\boldsymbol{\mathrm{n}}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{p}}\:\:\:\:\:\:=\:\underset{{n}\rightarrow\infty} {\boldsymbol{\mathrm{lim}}}\:\frac{\underset{\boldsymbol{{r}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\boldsymbol{\sum}}}\sqrt{\frac{\boldsymbol{{r}}}{\boldsymbol{{n}}}}\:\:×\:\underset{\boldsymbol{{r}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\boldsymbol{\sum}}}\sqrt{\frac{\boldsymbol{{n}}}{\boldsymbol{{r}}}}}{\frac{\boldsymbol{{n}}^{\mathrm{2}} }{\boldsymbol{{n}}}\underset{\boldsymbol{{r}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\boldsymbol{\sum}}}\frac{\boldsymbol{{r}}}{\boldsymbol{{n}}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{p}}\:\:\:\:\:\:\:=\:\:\underset{{n}\rightarrow\infty} {\boldsymbol{\mathrm{lim}}}\:\frac{\frac{\mathrm{1}}{\boldsymbol{{n}}}\:\underset{\boldsymbol{{r}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\boldsymbol{\sum}}}\:\sqrt{\frac{\boldsymbol{{r}}}{\boldsymbol{{n}}}}\:\:×\:\frac{\mathrm{1}}{\boldsymbol{{n}}}\:\underset{\boldsymbol{{r}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\boldsymbol{\sum}}}\:\sqrt{\frac{\boldsymbol{{n}}}{\boldsymbol{{r}}}}}{\frac{\mathrm{1}}{\boldsymbol{{n}}}\:\underset{\boldsymbol{{r}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\boldsymbol{\sum}}}\:\frac{\boldsymbol{{r}}}{\boldsymbol{{n}}}} \\ $$$$\:\:\:\:{let} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\boldsymbol{{r}}}{\boldsymbol{{n}}}\:=\:\boldsymbol{{x}}\:\:\:\:\:\boldsymbol{{if}}\:\:\boldsymbol{{r}}=\mathrm{1}\:\boldsymbol{{then}}\:\boldsymbol{{x}}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{and}}\:\boldsymbol{{r}}\:=\:\boldsymbol{{n}}\:\boldsymbol{{then}}\:\boldsymbol{{x}}\:=\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{p}}\:\:\:\:=\:\:\underset{{n}\rightarrow\infty} {\boldsymbol{\mathrm{lim}}}\frac{\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\boldsymbol{{x}}}\boldsymbol{{dx}}×\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\boldsymbol{{x}}}}\boldsymbol{{dx}}}{\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{{x}}\:\boldsymbol{{dx}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{p}}\:\:\:\:\:=\:\:\underset{{n}\rightarrow\infty} {\boldsymbol{\mathrm{lim}}}\:\frac{\frac{\boldsymbol{{x}}^{\mathrm{3}/\mathrm{2}} }{\mathrm{3}/\mathrm{2}}\mid_{\mathrm{0}} ^{\mathrm{1}} \:×\frac{\sqrt{\boldsymbol{{x}}}}{\mathrm{1}/\mathrm{2}}\mid_{\mathrm{0}} ^{ } }{\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{2}}\mid_{\mathrm{0}} ^{\mathrm{1}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{p}}\:\:\:=\:\:\frac{\mathrm{8}}{\mathrm{3}} \\ $$
Answered by Mathspace last updated on 01/May/22
![A_n =(((Σ_(k=1) ^n (√k))(Σ_(k=1) ^n (1/( (√k)))))/((n(n+1))/2)) =(2/(n^2 (1+(1/n))))(Σ...)(Σ...) ⇒lim_(n→+∞) A_n =2lim_(n→+∞) ((1/n)Σ(√k))((1/n)Σ(1/( (√k)))) =2lim_(n→+∞) ((1/n)Σ(√(k/n)))((1/n)Σ(1/( (√(k/n))))) =2∫_0 ^1 (√x)dx×∫_0 ^1 (dx/( (√x))) =2[(2/3)x^(3/2) ]_0 ^1 ×[2(√x)]_0 ^1 =(4/3)×2=(8/3)](https://www.tinkutara.com/question/Q169525.png)
$${A}_{{n}} =\frac{\left(\sum_{{k}=\mathrm{1}} ^{{n}} \sqrt{{k}}\right)\left(\sum_{{k}=\mathrm{1}} ^{{n}} \frac{\mathrm{1}}{\:\sqrt{{k}}}\right)}{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{2}}{{n}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)}\left(\Sigma…\right)\left(\Sigma…\right) \\ $$$$\Rightarrow{lim}_{{n}\rightarrow+\infty} {A}_{{n}} =\mathrm{2}{lim}_{{n}\rightarrow+\infty} \left(\frac{\mathrm{1}}{{n}}\Sigma\sqrt{{k}}\right)\left(\frac{\mathrm{1}}{{n}}\Sigma\frac{\mathrm{1}}{\:\sqrt{{k}}}\right) \\ $$$$=\mathrm{2}{lim}_{{n}\rightarrow+\infty} \left(\frac{\mathrm{1}}{{n}}\Sigma\sqrt{\frac{{k}}{{n}}}\right)\left(\frac{\mathrm{1}}{{n}}\Sigma\frac{\mathrm{1}}{\:\sqrt{\frac{{k}}{{n}}}}\right) \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}}{dx}×\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{{x}}} \\ $$$$=\mathrm{2}\left[\frac{\mathrm{2}}{\mathrm{3}}{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\mathrm{1}} ×\left[\mathrm{2}\sqrt{{x}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}×\mathrm{2}=\frac{\mathrm{8}}{\mathrm{3}} \\ $$
