Question-169610

Question Number 169610 by mathlove last updated on 04/May/22

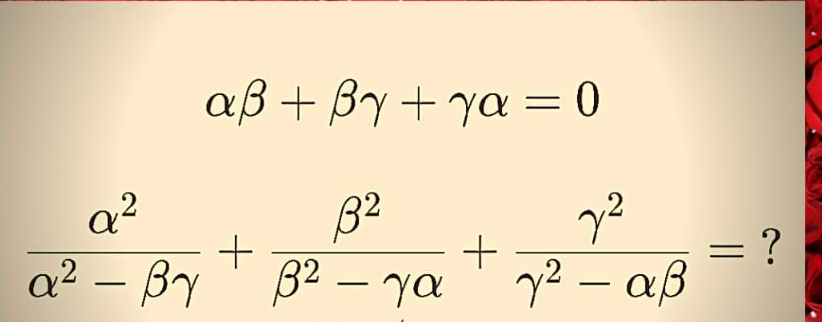
Answered by som(math1967) last updated on 04/May/22

\frac{α^{2}}{α^{2} + α β + α γ} + \frac{β^{2}}{β^{2} + α β + β γ} + \frac{γ^{2}}{γ^{2} + β γ + γ α} ★

= \frac{α^{2}}{α (α + β + γ)} + \frac{β^{2}}{β (α + β + γ)} + \frac{γ^{2}}{γ (α + β + γ)}

= \frac{(α + β + γ)}{(α + β + γ)} = 1 [α + β + γ \neq 0]

★ α β + β γ + γ α = 0

∴ - β γ = α β + α γ

- γ α = α β + β γ

- α β = β γ + γ α