Question-169626

Question Number 169626 by Shrinava last updated on 04/May/22

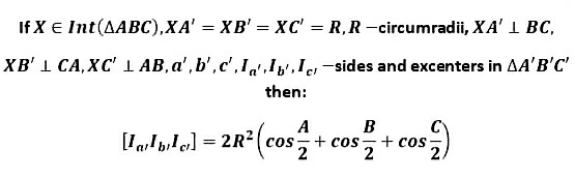
Answered by mr W last updated on 04/May/22

Commented by mr W last updated on 04/May/22

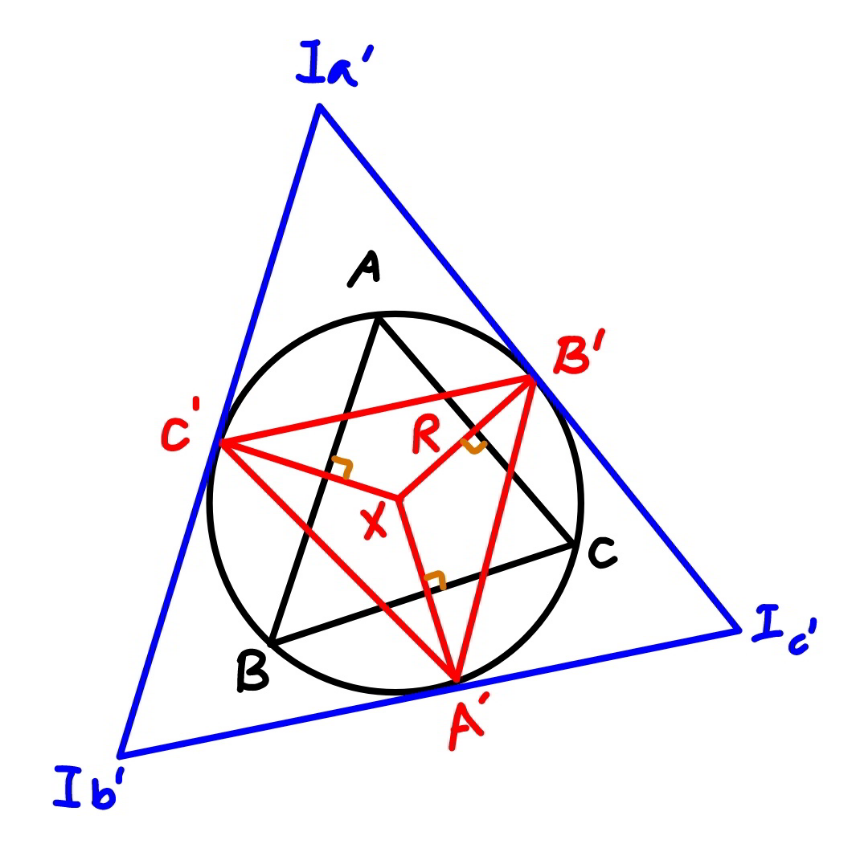
a′=B′C′=2R sin ((π−A)/2)=2R sin A′ ⇒A′=(π/2)−(A/2) ⇒sin A′=cos (A/2) similarly ⇒B′=(π/2)−(B/2) ⇒sin B′=cos (B/2) ⇒C′=(π/2)−(C/2) ⇒sin C′=cos (C/2) [I_(a′) I_(b′) I_(c′) ]=8R^2 cos ((A′)/2)cos ((B′)/2)cos ((C′)/2) [I_(a′) I_(b′) I_(c′) ]=2R^2 (sin A′+sin B′+sin C′) [I_(a′) I_(b′) I_(c′) ]=2R^2 (cos (A/2)+cos (B/2)+cos (C/2)) ✓

$${a}'={B}'{C}'=\mathrm{2}{R}\:\mathrm{sin}\:\frac{\pi−{A}}{\mathrm{2}}=\mathrm{2}{R}\:\mathrm{sin}\:{A}' \\ $$$$\Rightarrow{A}'=\frac{\pi}{\mathrm{2}}−\frac{{A}}{\mathrm{2}}\:\Rightarrow\mathrm{sin}\:{A}'=\mathrm{cos}\:\frac{{A}}{\mathrm{2}} \\ $$$${similarly} \\ $$$$\Rightarrow{B}'=\frac{\pi}{\mathrm{2}}−\frac{{B}}{\mathrm{2}}\:\Rightarrow\mathrm{sin}\:{B}'=\mathrm{cos}\:\frac{{B}}{\mathrm{2}} \\ $$$$\Rightarrow{C}'=\frac{\pi}{\mathrm{2}}−\frac{{C}}{\mathrm{2}}\:\Rightarrow\mathrm{sin}\:{C}'=\mathrm{cos}\:\frac{{C}}{\mathrm{2}} \\ $$$$\left[{I}_{{a}'} {I}_{{b}'} {I}_{{c}'} \right]=\mathrm{8}{R}^{\mathrm{2}} \mathrm{cos}\:\frac{{A}'}{\mathrm{2}}\mathrm{cos}\:\frac{{B}'}{\mathrm{2}}\mathrm{cos}\:\frac{{C}'}{\mathrm{2}} \\ $$$$\left[{I}_{{a}'} {I}_{{b}'} {I}_{{c}'} \right]=\mathrm{2}{R}^{\mathrm{2}} \left(\mathrm{sin}\:{A}'+\mathrm{sin}\:{B}'+\mathrm{sin}\:{C}'\right) \\ $$$$\left[{I}_{{a}'} {I}_{{b}'} {I}_{{c}'} \right]=\mathrm{2}{R}^{\mathrm{2}} \left(\mathrm{cos}\:\frac{{A}}{\mathrm{2}}+\mathrm{cos}\:\frac{{B}}{\mathrm{2}}+\mathrm{cos}\:\frac{{C}}{\mathrm{2}}\right)\:\checkmark \\ $$

Commented by MaxiMaths last updated on 05/May/22

please sir, which app do u use to make those figures ?

$$\mathrm{please}\:\mathrm{sir},\:\mathrm{which}\:\mathrm{app}\:\mathrm{do}\:\mathrm{u}\:\mathrm{use}\:\mathrm{to}\:\mathrm{make} \\ $$$$\mathrm{those}\:\mathrm{figures}\:? \\ $$

Commented by mr W last updated on 05/May/22