Question Number 169631 by MaxiMaths last updated on 05/May/22

Commented by MaxiMaths last updated on 05/May/22
$$\mathrm{any}\:\mathrm{way}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{function}\:{f}\:??? \\ $$
Commented by mr W last updated on 05/May/22
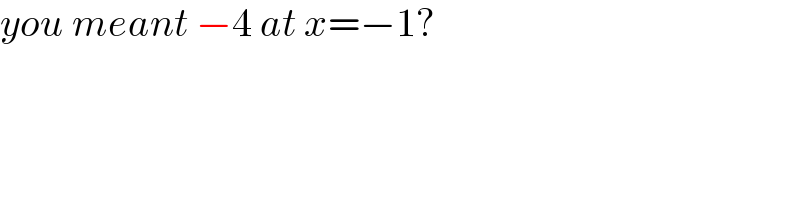
$${you}\:{meant}\:−\mathrm{4}\:{at}\:{x}=−\mathrm{1}? \\ $$
Commented by mr W last updated on 05/May/22

$${infinite}\:{possibilities}. \\ $$$${example}\:{f}\left({x}\right)=−\frac{\mathrm{14}}{\mathrm{9}}\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}{x}\right)−\frac{\mathrm{59}}{\mathrm{27}} \\ $$
Commented by mr W last updated on 05/May/22

Answered by mr W last updated on 05/May/22
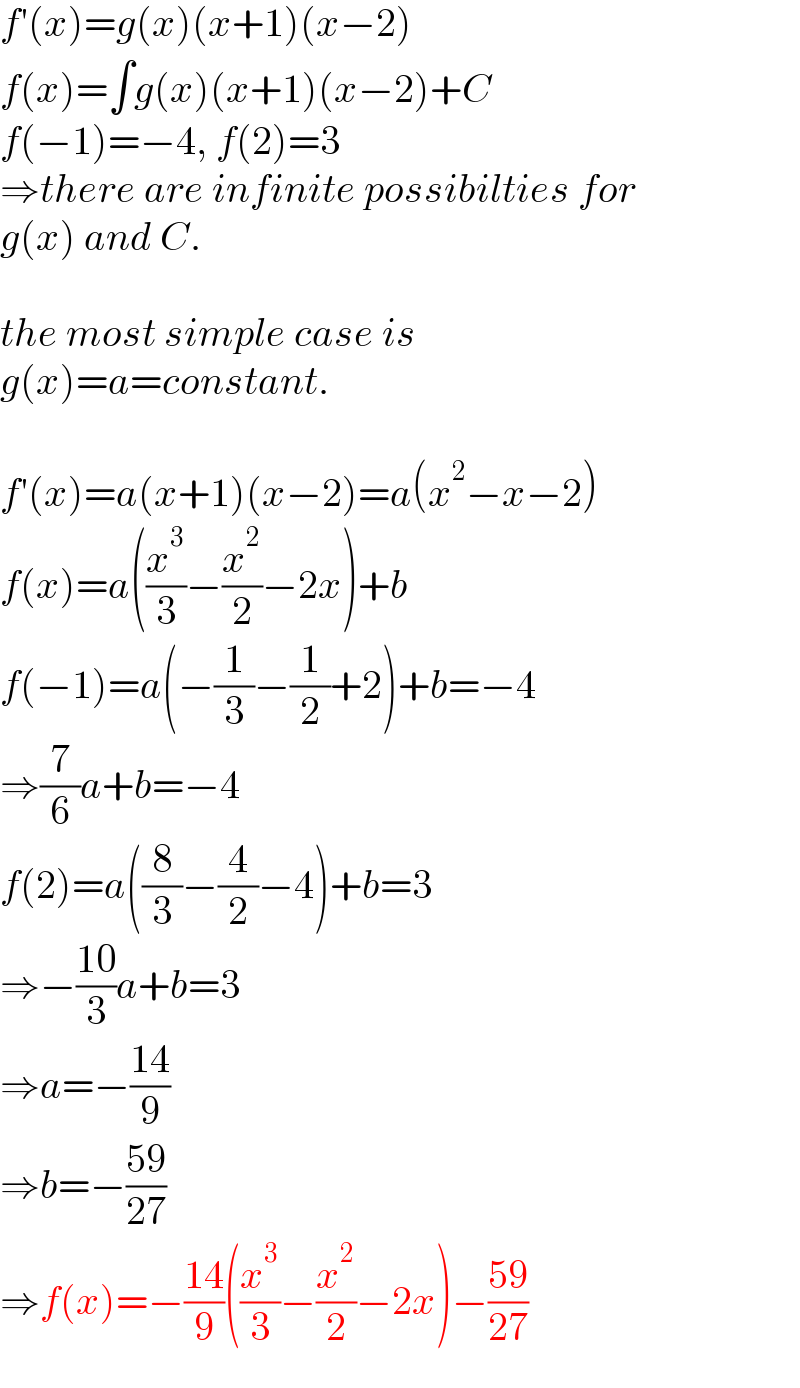
$${f}'\left({x}\right)={g}\left({x}\right)\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right) \\ $$$${f}\left({x}\right)=\int{g}\left({x}\right)\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)+{C} \\ $$$${f}\left(−\mathrm{1}\right)=−\mathrm{4},\:{f}\left(\mathrm{2}\right)=\mathrm{3} \\ $$$$\Rightarrow{there}\:{are}\:{infinite}\:{possibilties}\:{for} \\ $$$${g}\left({x}\right)\:{and}\:{C}. \\ $$$$ \\ $$$${the}\:{most}\:{simple}\:{case}\:{is}\: \\ $$$${g}\left({x}\right)={a}={constant}. \\ $$$$ \\ $$$${f}'\left({x}\right)={a}\left({x}+\mathrm{1}\right)\left({x}−\mathrm{2}\right)={a}\left({x}^{\mathrm{2}} −{x}−\mathrm{2}\right) \\ $$$${f}\left({x}\right)={a}\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}{x}\right)+{b} \\ $$$${f}\left(−\mathrm{1}\right)={a}\left(−\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{2}\right)+{b}=−\mathrm{4} \\ $$$$\Rightarrow\frac{\mathrm{7}}{\mathrm{6}}{a}+{b}=−\mathrm{4} \\ $$$${f}\left(\mathrm{2}\right)={a}\left(\frac{\mathrm{8}}{\mathrm{3}}−\frac{\mathrm{4}}{\mathrm{2}}−\mathrm{4}\right)+{b}=\mathrm{3} \\ $$$$\Rightarrow−\frac{\mathrm{10}}{\mathrm{3}}{a}+{b}=\mathrm{3} \\ $$$$\Rightarrow{a}=−\frac{\mathrm{14}}{\mathrm{9}} \\ $$$$\Rightarrow{b}=−\frac{\mathrm{59}}{\mathrm{27}} \\ $$$$\Rightarrow{f}\left({x}\right)=−\frac{\mathrm{14}}{\mathrm{9}}\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}{x}\right)−\frac{\mathrm{59}}{\mathrm{27}} \\ $$
Commented by MaxiMaths last updated on 06/May/22

$$\mathrm{waoh}\:!\:\mathrm{good}\:! \\ $$
