Question Number 169756 by mokys last updated on 07/May/22

Answered by aleks041103 last updated on 07/May/22
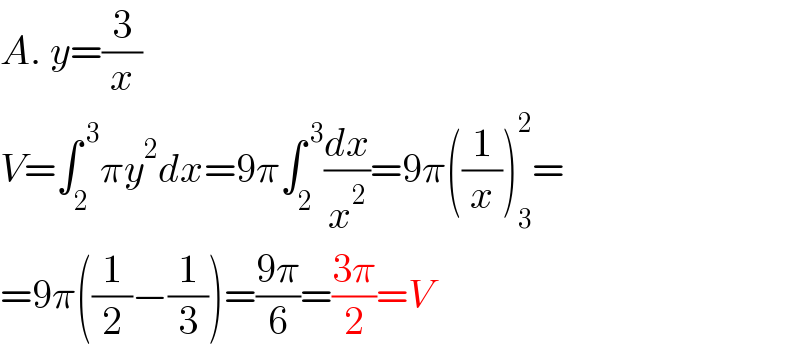
$${A}.\:{y}=\frac{\mathrm{3}}{{x}} \\ $$$${V}=\int_{\mathrm{2}} ^{\:\mathrm{3}} \pi{y}^{\mathrm{2}} {dx}=\mathrm{9}\pi\int_{\mathrm{2}} ^{\:\mathrm{3}} \frac{{dx}}{{x}^{\mathrm{2}} }=\mathrm{9}\pi\left(\frac{\mathrm{1}}{{x}}\right)_{\mathrm{3}} ^{\mathrm{2}} = \\ $$$$=\mathrm{9}\pi\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{9}\pi}{\mathrm{6}}=\frac{\mathrm{3}\pi}{\mathrm{2}}={V} \\ $$
Answered by aleks041103 last updated on 07/May/22
![B. (a) V=∫_0 ^( 3) πy^2 dx=π∫_0 ^( 3) (2x^2 +3)^2 dx= =π∫_0 ^( 3) (4x^4 +12x^2 +9)dx= =π[(4/5)x^5 +4x^3 +9x]_0 ^3 = =π(((4.3^5 )/5)+4.3^3 +9.3)= =π(((36.3^3 )/5)+5.3^3 )= =((27π)/5)(36+25)=((27.61π)/5)](https://www.tinkutara.com/question/Q169762.png)
$${B}. \\ $$$$\left({a}\right)\:{V}=\int_{\mathrm{0}} ^{\:\mathrm{3}} \pi{y}^{\mathrm{2}} {dx}=\pi\int_{\mathrm{0}} ^{\:\mathrm{3}} \left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} {dx}= \\ $$$$=\pi\int_{\mathrm{0}} ^{\:\mathrm{3}} \left(\mathrm{4}{x}^{\mathrm{4}} +\mathrm{12}{x}^{\mathrm{2}} +\mathrm{9}\right){dx}= \\ $$$$=\pi\left[\frac{\mathrm{4}}{\mathrm{5}}{x}^{\mathrm{5}} +\mathrm{4}{x}^{\mathrm{3}} +\mathrm{9}{x}\right]_{\mathrm{0}} ^{\mathrm{3}} = \\ $$$$=\pi\left(\frac{\mathrm{4}.\mathrm{3}^{\mathrm{5}} }{\mathrm{5}}+\mathrm{4}.\mathrm{3}^{\mathrm{3}} +\mathrm{9}.\mathrm{3}\right)= \\ $$$$=\pi\left(\frac{\mathrm{36}.\mathrm{3}^{\mathrm{3}} }{\mathrm{5}}+\mathrm{5}.\mathrm{3}^{\mathrm{3}} \right)= \\ $$$$=\frac{\mathrm{27}\pi}{\mathrm{5}}\left(\mathrm{36}+\mathrm{25}\right)=\frac{\mathrm{27}.\mathrm{61}\pi}{\mathrm{5}} \\ $$
Answered by thfchristopher last updated on 08/May/22
![A. For the curve rotates x-axis, y=(3/x) V=π∫_2 ^3 ((3/x))^2 dx =π∫_2 ^3 (9/x^2 )dx =−π[(9/x)]_2 ^3 =((3π)/2) B. (a) For the curve rotates x-axis, V_x =π∫_0 ^3 (2x^2 +3)^2 dx =π∫_0 ^3 (4x^4 +12x^2 +9)dx =π[((4x^5 )/5)+4x^3 +9x]_0 ^3 =((783π)/5) (b) For the curve rotates y-axis, x=(√((y−3)/2)) When x=3, y=21 x=0, y=3 ∴ V_y =π∫_3 ^(21) ((y−3)/2)dy =π[(y^2 /4)−((3y)/2)]_3 ^(21) =81π](https://www.tinkutara.com/question/Q169796.png)
$$\mathrm{A}. \\ $$$$\mathrm{For}\:\mathrm{the}\:\mathrm{curve}\:\mathrm{rotates}\:\mathrm{x}-\mathrm{axis}, \\ $$$${y}=\frac{\mathrm{3}}{{x}} \\ $$$${V}=\pi\int_{\mathrm{2}} ^{\mathrm{3}} \left(\frac{\mathrm{3}}{{x}}\right)^{\mathrm{2}} {dx} \\ $$$$=\pi\int_{\mathrm{2}} ^{\mathrm{3}} \frac{\mathrm{9}}{{x}^{\mathrm{2}} }{dx} \\ $$$$=−\pi\left[\frac{\mathrm{9}}{{x}}\right]_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$=\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{B}. \\ $$$$\left(\mathrm{a}\right)\:\mathrm{For}\:\mathrm{the}\:\mathrm{curve}\:\mathrm{rotates}\:\mathrm{x}-\mathrm{axis}, \\ $$$${V}_{{x}} =\pi\int_{\mathrm{0}} ^{\mathrm{3}} \left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} {dx} \\ $$$$=\pi\int_{\mathrm{0}} ^{\mathrm{3}} \left(\mathrm{4}{x}^{\mathrm{4}} +\mathrm{12}{x}^{\mathrm{2}} +\mathrm{9}\right){dx} \\ $$$$=\pi\left[\frac{\mathrm{4}{x}^{\mathrm{5}} }{\mathrm{5}}+\mathrm{4}{x}^{\mathrm{3}} +\mathrm{9}{x}\right]_{\mathrm{0}} ^{\mathrm{3}} \\ $$$$=\frac{\mathrm{783}\pi}{\mathrm{5}} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{For}\:\mathrm{the}\:\mathrm{curve}\:\mathrm{rotates}\:\mathrm{y}-\mathrm{axis}, \\ $$$${x}=\sqrt{\frac{{y}−\mathrm{3}}{\mathrm{2}}} \\ $$$$\mathrm{When}\:{x}=\mathrm{3},\:{y}=\mathrm{21} \\ $$$${x}=\mathrm{0},\:{y}=\mathrm{3} \\ $$$$\therefore\:{V}_{{y}} =\pi\int_{\mathrm{3}} ^{\mathrm{21}} \frac{{y}−\mathrm{3}}{\mathrm{2}}{dy} \\ $$$$=\pi\left[\frac{{y}^{\mathrm{2}} }{\mathrm{4}}−\frac{\mathrm{3}{y}}{\mathrm{2}}\right]_{\mathrm{3}} ^{\mathrm{21}} \\ $$$$=\mathrm{81}\pi \\ $$
