Question-169774

Facebook Tweet Pin

Question Number 169774 by mr W last updated on 08/May/22

Commented by cortano1 last updated on 08/May/22

$${what}\:{this}\:{answer}? \\ $$

Commented by mr W last updated on 08/May/22

Commented by mr W last updated on 08/May/22

point C which fulfills AC+BC≤10 must lie on or inside the ellipse with A and B as foci. so the probability is p=((area of green ellipse)/(area of red square)). eqn. of ellipse is (x^2 /5^2 )+(y^2 /3^2 )=1, its area is π×3×5=15π. the area of square is 20^2 =400. ⇒p=((15π)/(400))=((3π)/(80))≈11.8%

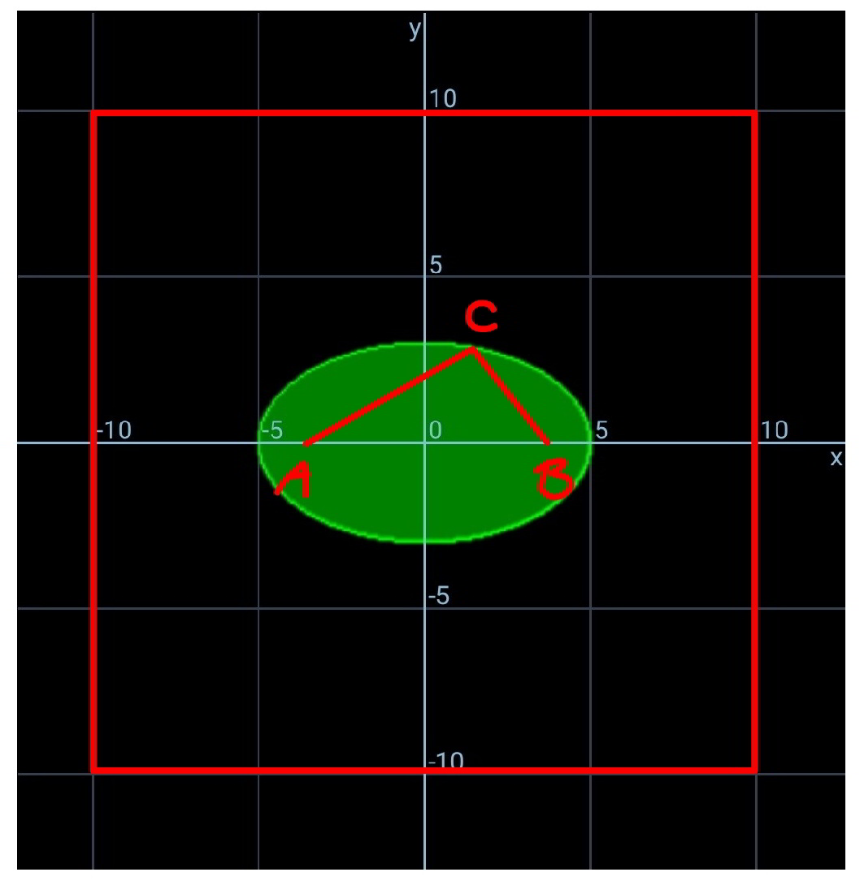
$${point}\:{C}\:{which}\:{fulfills}\:{AC}+{BC}\leqslant\mathrm{10} \\ $$$${must}\:{lie}\:{on}\:{or}\:{inside}\:{the}\:{ellipse} \\ $$$${with}\:{A}\:{and}\:{B}\:{as}\:{foci}.\:{so}\:{the}\:{probability} \\ $$$${is}\:{p}=\frac{{area}\:{of}\:{green}\:{ellipse}}{{area}\:{of}\:{red}\:{square}}. \\ $$$${eqn}.\:{of}\:{ellipse}\:{is}\:\frac{{x}^{\mathrm{2}} }{\mathrm{5}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{2}} }=\mathrm{1},\:{its}\:{area} \\ $$$${is}\:\pi×\mathrm{3}×\mathrm{5}=\mathrm{15}\pi. \\ $$$${the}\:{area}\:{of}\:{square}\:{is}\:\mathrm{20}^{\mathrm{2}} =\mathrm{400}. \\ $$$$\Rightarrow{p}=\frac{\mathrm{15}\pi}{\mathrm{400}}=\frac{\mathrm{3}\pi}{\mathrm{80}}\approx\mathrm{11}.\mathrm{8\%} \\ $$

Answered by cortano1 last updated on 08/May/22

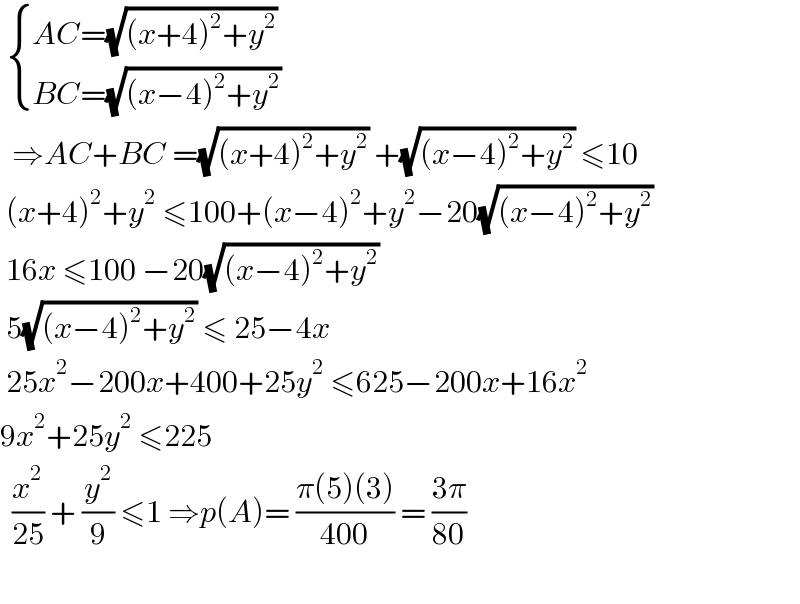
{ ((AC=(√((x+4)^2 +y^2 )))),((BC=(√((x−4)^2 +y^2 )))) :} ⇒AC+BC =(√((x+4)^2 +y^2 )) +(√((x−4)^2 +y^2 )) ≤10 (x+4)^2 +y^2 ≤100+(x−4)^2 +y^2 −20(√((x−4)^2 +y^2 )) 16x ≤100 −20(√((x−4)^2 +y^2 )) 5(√((x−4)^2 +y^2 )) ≤ 25−4x 25x^2 −200x+400+25y^2 ≤625−200x+16x^2 9x^2 +25y^2 ≤225 (x^2 /(25)) + (y^2 /9) ≤1 ⇒p(A)= ((π(5)(3))/(400)) = ((3π)/(80))

$$\:\begin{cases}{{AC}=\sqrt{\left({x}+\mathrm{4}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }}\\{{BC}=\sqrt{\left({x}−\mathrm{4}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }}\end{cases}\: \\ $$$$\:\:\Rightarrow{AC}+{BC}\:=\sqrt{\left({x}+\mathrm{4}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }\:+\sqrt{\left({x}−\mathrm{4}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\leqslant\mathrm{10} \\ $$$$\:\left({x}+\mathrm{4}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \:\leqslant\mathrm{100}+\left({x}−\mathrm{4}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{20}\sqrt{\left({x}−\mathrm{4}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$\:\mathrm{16}{x}\:\leqslant\mathrm{100}\:−\mathrm{20}\sqrt{\left({x}−\mathrm{4}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$$\:\mathrm{5}\sqrt{\left({x}−\mathrm{4}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\leqslant\:\mathrm{25}−\mathrm{4}{x} \\ $$$$\:\mathrm{25}{x}^{\mathrm{2}} −\mathrm{200}{x}+\mathrm{400}+\mathrm{25}{y}^{\mathrm{2}} \:\leqslant\mathrm{625}−\mathrm{200}{x}+\mathrm{16}{x}^{\mathrm{2}} \\ $$$$\mathrm{9}{x}^{\mathrm{2}} +\mathrm{25}{y}^{\mathrm{2}} \:\leqslant\mathrm{225}\: \\ $$$$\:\:\frac{{x}^{\mathrm{2}} }{\mathrm{25}}\:+\:\frac{{y}^{\mathrm{2}} }{\mathrm{9}}\:\leqslant\mathrm{1}\:\Rightarrow{p}\left({A}\right)=\:\frac{\pi\left(\mathrm{5}\right)\left(\mathrm{3}\right)}{\mathrm{400}}\:=\:\frac{\mathrm{3}\pi}{\mathrm{80}} \\ $$$$\: \\ $$

Commented by mr W last updated on 08/May/22