Question Number 169821 by cortano1 last updated on 10/May/22
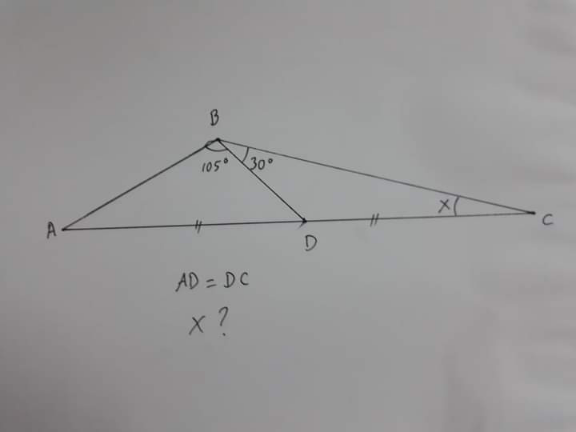
Answered by floor(10²Eta[1]) last updated on 10/May/22
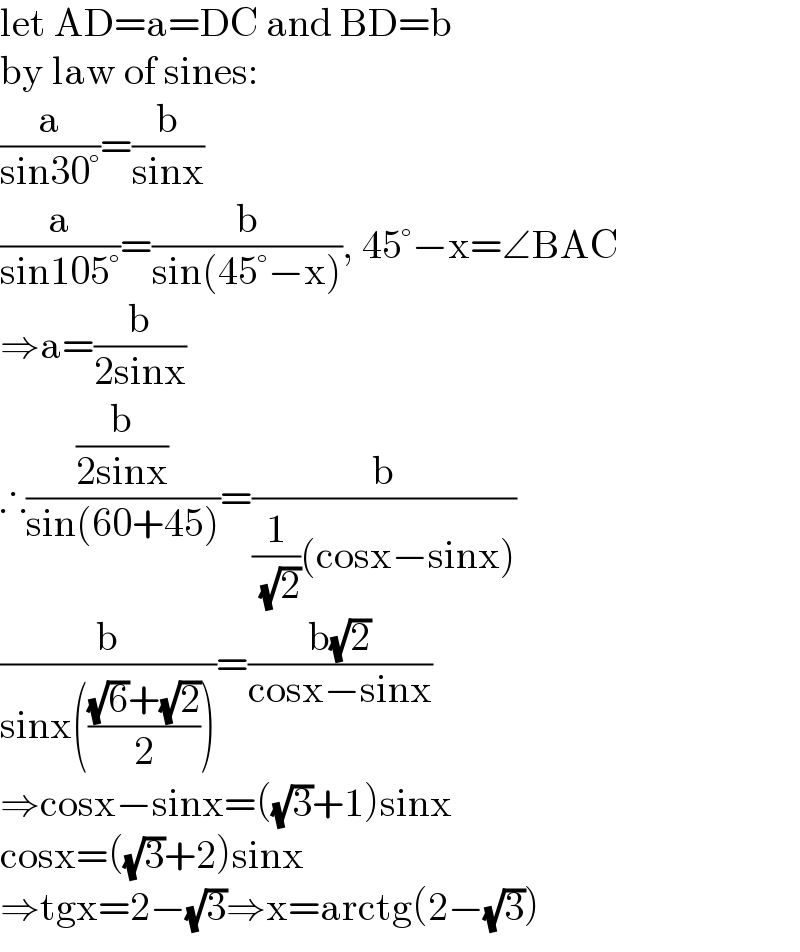
$$\mathrm{let}\:\mathrm{AD}=\mathrm{a}=\mathrm{DC}\:\mathrm{and}\:\mathrm{BD}=\mathrm{b} \\ $$$$\mathrm{by}\:\mathrm{law}\:\mathrm{of}\:\mathrm{sines}: \\ $$$$\frac{\mathrm{a}}{\mathrm{sin30}°}=\frac{\mathrm{b}}{\mathrm{sinx}}\: \\ $$$$\frac{\mathrm{a}}{\mathrm{sin105}°}=\frac{\mathrm{b}}{\mathrm{sin}\left(\mathrm{45}°−\mathrm{x}\right)},\:\mathrm{45}°−\mathrm{x}=\angle\mathrm{BAC} \\ $$$$\Rightarrow\mathrm{a}=\frac{\mathrm{b}}{\mathrm{2sinx}} \\ $$$$\therefore\frac{\frac{\mathrm{b}}{\mathrm{2sinx}}}{\mathrm{sin}\left(\mathrm{60}+\mathrm{45}\right)}=\frac{\mathrm{b}}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{cosx}−\mathrm{sinx}\right)} \\ $$$$\frac{\mathrm{b}}{\mathrm{sinx}\left(\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{2}}\right)}=\frac{\mathrm{b}\sqrt{\mathrm{2}}}{\mathrm{cosx}−\mathrm{sinx}} \\ $$$$\Rightarrow\mathrm{cosx}−\mathrm{sinx}=\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)\mathrm{sinx} \\ $$$$\mathrm{cosx}=\left(\sqrt{\mathrm{3}}+\mathrm{2}\right)\mathrm{sinx} \\ $$$$\Rightarrow\mathrm{tgx}=\mathrm{2}−\sqrt{\mathrm{3}}\Rightarrow\mathrm{x}=\mathrm{arctg}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right) \\ $$
Answered by bobhans last updated on 10/May/22
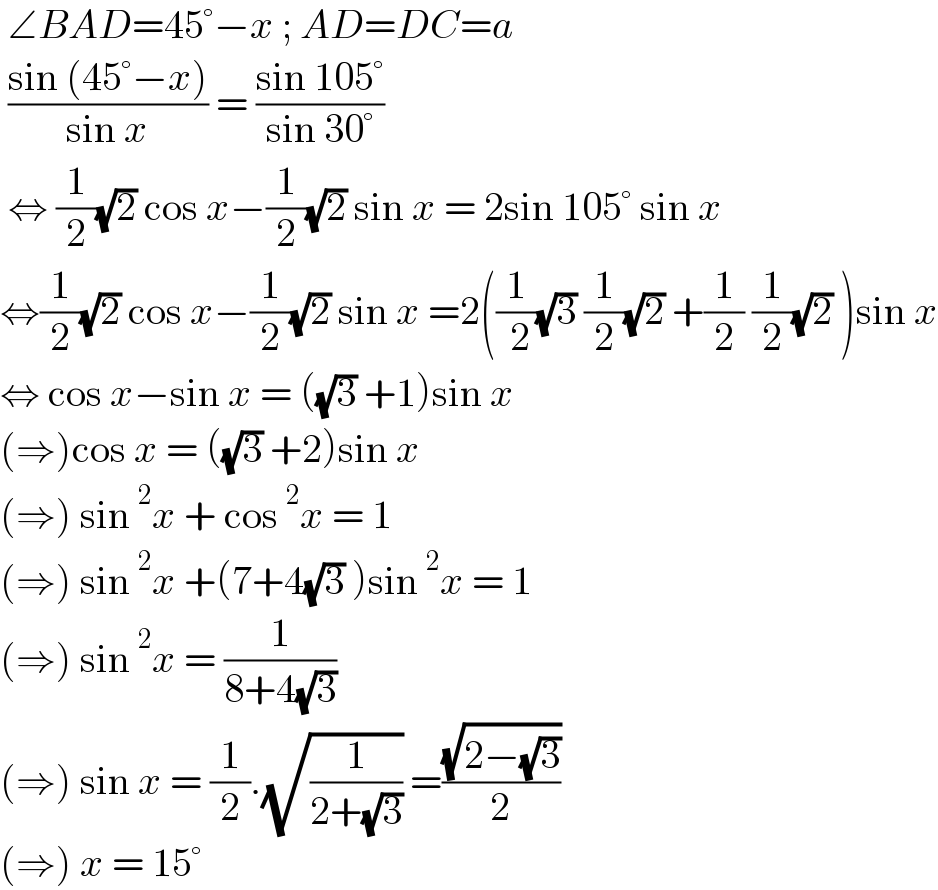
$$\:\angle{BAD}=\mathrm{45}°−{x}\:;\:{AD}={DC}={a} \\ $$$$\:\frac{\mathrm{sin}\:\left(\mathrm{45}°−{x}\right)}{\mathrm{sin}\:{x}}\:=\:\frac{\mathrm{sin}\:\mathrm{105}°}{\mathrm{sin}\:\mathrm{30}°} \\ $$$$\:\Leftrightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}}\:\mathrm{cos}\:{x}−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}}\:\mathrm{sin}\:{x}\:=\:\mathrm{2sin}\:\mathrm{105}°\:\mathrm{sin}\:{x} \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}}\:\mathrm{cos}\:{x}−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}}\:\mathrm{sin}\:{x}\:=\mathrm{2}\left(\frac{\mathrm{1}}{\:\mathrm{2}}\sqrt{\mathrm{3}}\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}}\:\right)\mathrm{sin}\:{x} \\ $$$$\Leftrightarrow\:\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\:=\:\left(\sqrt{\mathrm{3}}\:+\mathrm{1}\right)\mathrm{sin}\:{x} \\ $$$$\left(\Rightarrow\right)\mathrm{cos}\:{x}\:=\:\left(\sqrt{\mathrm{3}}\:+\mathrm{2}\right)\mathrm{sin}\:{x} \\ $$$$\left(\Rightarrow\right)\:\mathrm{sin}\:^{\mathrm{2}} {x}\:+\:\mathrm{cos}\:^{\mathrm{2}} {x}\:=\:\mathrm{1} \\ $$$$\left(\Rightarrow\right)\:\mathrm{sin}\:^{\mathrm{2}} {x}\:+\left(\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}\:\right)\mathrm{sin}\:^{\mathrm{2}} {x}\:=\:\mathrm{1} \\ $$$$\left(\Rightarrow\right)\:\mathrm{sin}\:^{\mathrm{2}} {x}\:=\:\frac{\mathrm{1}}{\mathrm{8}+\mathrm{4}\sqrt{\mathrm{3}}} \\ $$$$\left(\Rightarrow\right)\:\mathrm{sin}\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}.\sqrt{\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{3}}}}\:=\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{2}} \\ $$$$\left(\Rightarrow\right)\:{x}\:=\:\mathrm{15}°\: \\ $$
Commented by cortano1 last updated on 10/May/22
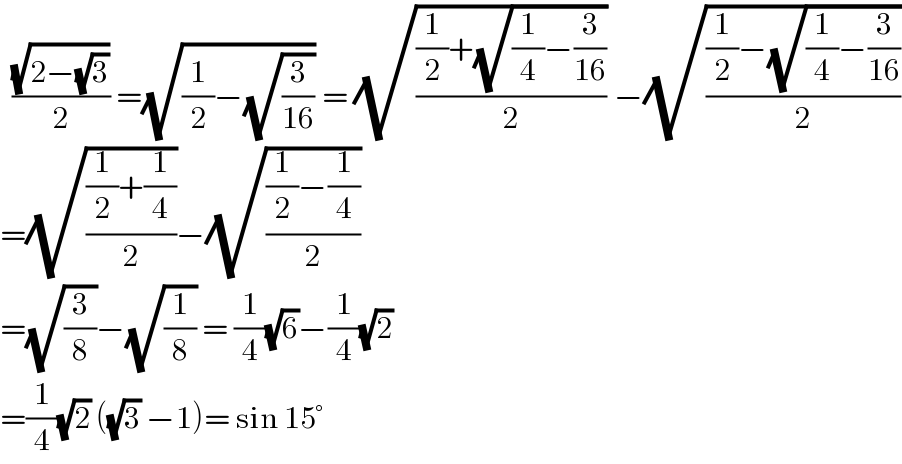
$$\:\:\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{2}}\:=\sqrt{\frac{\mathrm{1}}{\mathrm{2}}−\sqrt{\frac{\mathrm{3}}{\mathrm{16}}}}\:=\:\sqrt{\frac{\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{16}}}}{\mathrm{2}}}\:−\sqrt{\frac{\frac{\mathrm{1}}{\mathrm{2}}−\sqrt{\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{16}}}}{\mathrm{2}}} \\ $$$$=\sqrt{\frac{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{2}}}−\sqrt{\frac{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{2}}} \\ $$$$=\sqrt{\frac{\mathrm{3}}{\mathrm{8}}}−\sqrt{\frac{\mathrm{1}}{\mathrm{8}}}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{2}}\:\left(\sqrt{\mathrm{3}}\:−\mathrm{1}\right)=\:\mathrm{sin}\:\mathrm{15}° \\ $$
