Question Number 169825 by mathlove last updated on 10/May/22
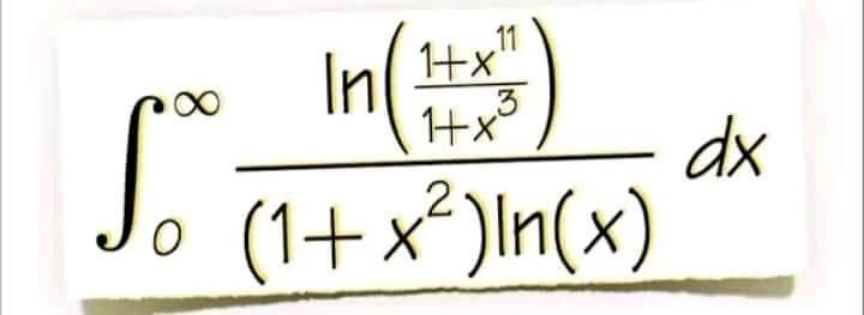
Answered by Mathspace last updated on 10/May/22

$${I}=_{{x}=\frac{\mathrm{1}}{{t}}} \:\:\:−\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{11}} }}{\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{3}} }}\right)}{\left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)\left(−{lnt}\right)}\left(−\frac{{dt}}{{t}^{\mathrm{2}} }\right) \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left({t}^{−\mathrm{8}} \left(\frac{\mathrm{1}+{t}^{\mathrm{11}} }{\mathrm{1}+{t}^{\mathrm{3}} }\right)\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right){lnt}}{dt} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left(\frac{\mathrm{1}+{t}^{\mathrm{11}} }{\mathrm{1}+{t}^{\mathrm{3}} }\right)}{\left({t}^{\mathrm{2}} +\mathrm{1}\right){lnt}}{dt}+\mathrm{8}\int_{\mathrm{0}} ^{\infty} \frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=−{I}+\mathrm{8}.\frac{\pi}{\mathrm{2}}=−{I}+\mathrm{4}\pi\:\Rightarrow \\ $$$$\mathrm{2}{I}=\mathrm{4}\pi\:\Rightarrow{I}=\mathrm{2}\pi \\ $$
