Question Number 169849 by cherokeesay last updated on 10/May/22
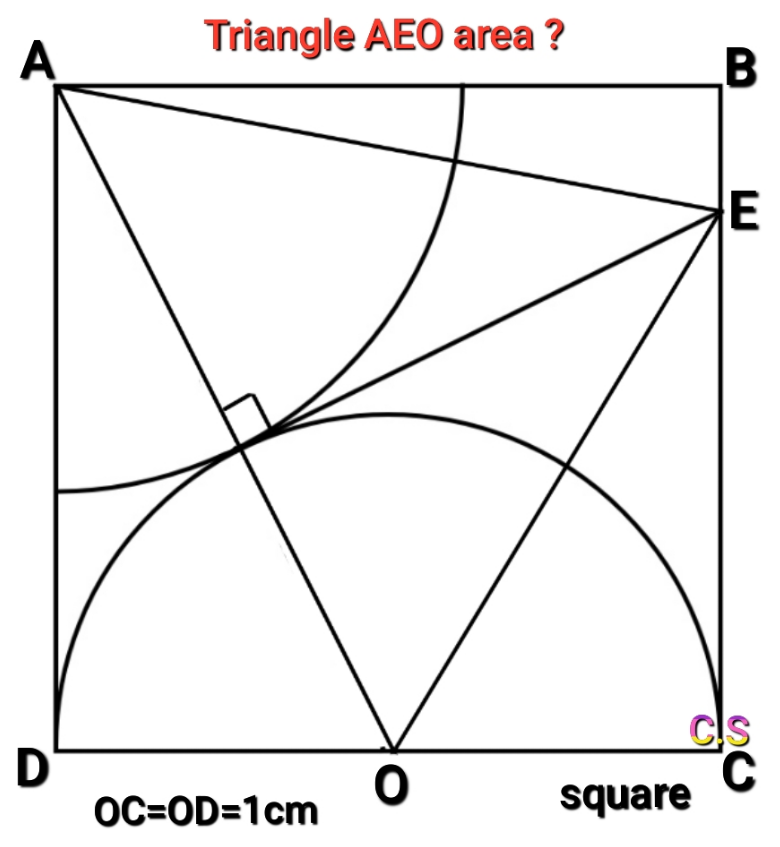
Answered by som(math1967) last updated on 11/May/22
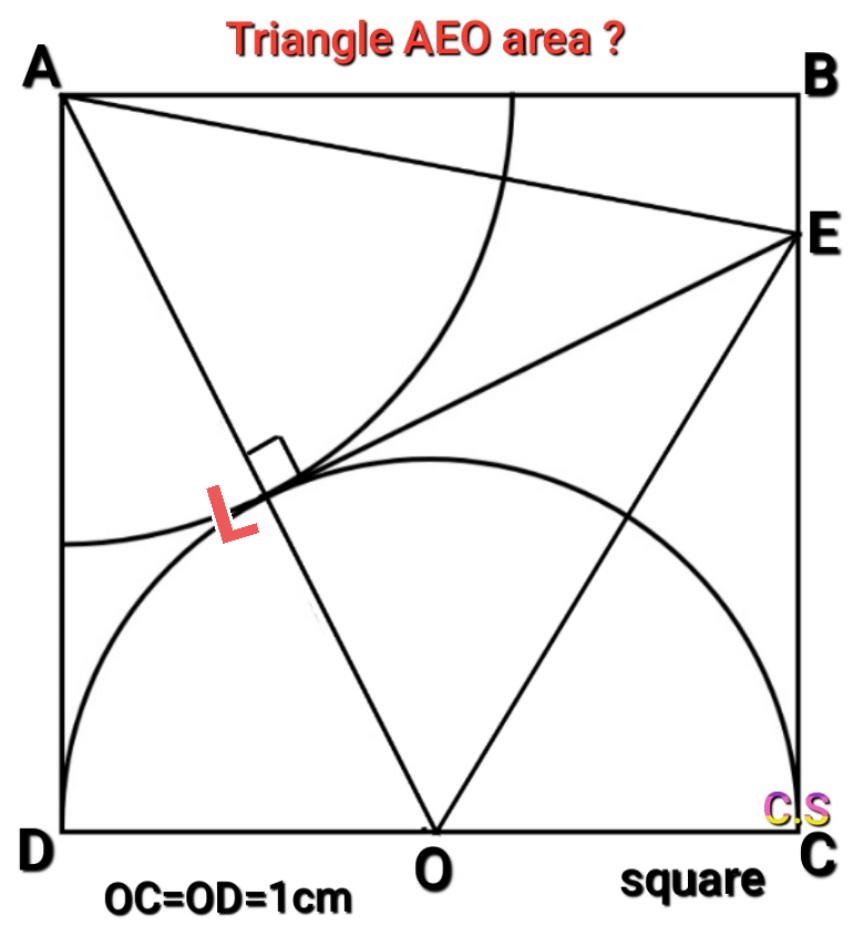
Commented by som(math1967) last updated on 11/May/22
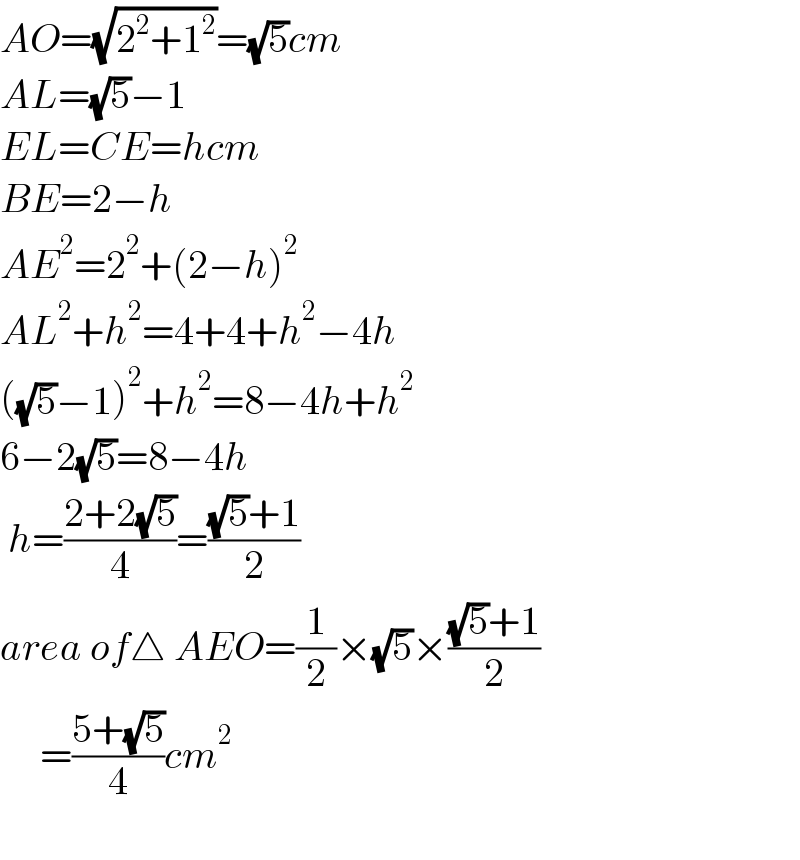
$${AO}=\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }=\sqrt{\mathrm{5}}{cm} \\ $$$${AL}=\sqrt{\mathrm{5}}−\mathrm{1} \\ $$$${EL}={CE}={hcm} \\ $$$${BE}=\mathrm{2}−{h} \\ $$$${AE}^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} +\left(\mathrm{2}−{h}\right)^{\mathrm{2}} \\ $$$${AL}^{\mathrm{2}} +{h}^{\mathrm{2}} =\mathrm{4}+\mathrm{4}+{h}^{\mathrm{2}} −\mathrm{4}{h} \\ $$$$\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)^{\mathrm{2}} +{h}^{\mathrm{2}} =\mathrm{8}−\mathrm{4}{h}+{h}^{\mathrm{2}} \\ $$$$\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}=\mathrm{8}−\mathrm{4}{h} \\ $$$$\:{h}=\frac{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}} \\ $$$${area}\:{of}\bigtriangleup\:{AEO}=\frac{\mathrm{1}}{\mathrm{2}}×\sqrt{\mathrm{5}}×\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:=\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{4}}{cm}^{\mathrm{2}} \\ $$$$ \\ $$
Commented by cherokeesay last updated on 11/May/22

$${greet}\:! \\ $$$${thank}\:{you}\:{sir}\:! \\ $$
