Question Number 169864 by mathlove last updated on 11/May/22

Answered by Mathspace last updated on 11/May/22
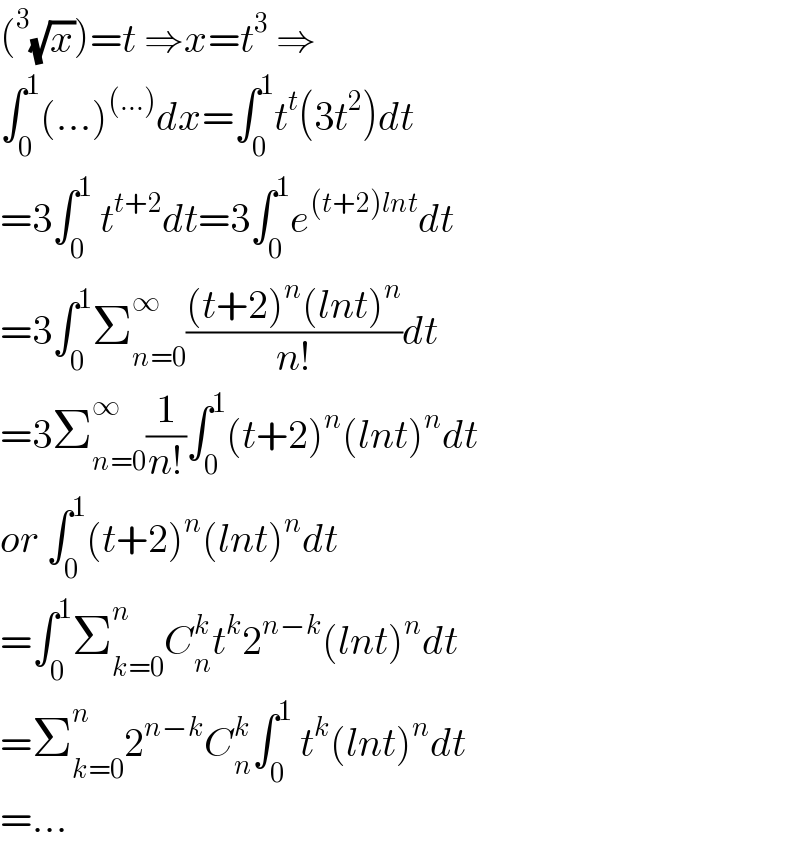
$$\left(^{\mathrm{3}} \sqrt{{x}}\right)={t}\:\Rightarrow{x}={t}^{\mathrm{3}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(…\right)^{\left(…\right)} {dx}=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{t}} \left(\mathrm{3}{t}^{\mathrm{2}} \right){dt} \\ $$$$=\mathrm{3}\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{t}+\mathrm{2}} {dt}=\mathrm{3}\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{\left({t}+\mathrm{2}\right){lnt}} {dt} \\ $$$$=\mathrm{3}\int_{\mathrm{0}} ^{\mathrm{1}} \sum_{{n}=\mathrm{0}} ^{\infty} \frac{\left({t}+\mathrm{2}\right)^{{n}} \left({lnt}\right)^{{n}} }{{n}!}{dt} \\ $$$$=\mathrm{3}\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{n}!}\int_{\mathrm{0}} ^{\mathrm{1}} \left({t}+\mathrm{2}\right)^{{n}} \left({lnt}\right)^{{n}} {dt} \\ $$$${or}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left({t}+\mathrm{2}\right)^{{n}} \left({lnt}\right)^{{n}} {dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \sum_{{k}=\mathrm{0}} ^{{n}} {C}_{{n}} ^{{k}} {t}^{{k}} \mathrm{2}^{{n}−{k}} \left({lnt}\right)^{{n}} {dt} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}} \mathrm{2}^{{n}−{k}} {C}_{{n}} ^{{k}} \int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{{k}} \left({lnt}\right)^{{n}} {dt} \\ $$$$=… \\ $$
