Question Number 169878 by mathlove last updated on 11/May/22
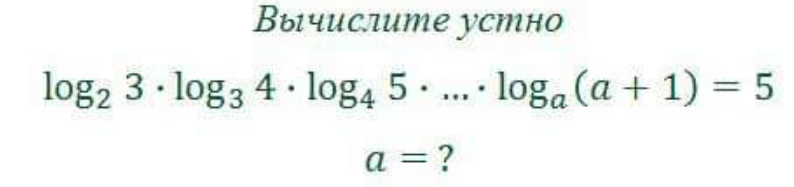
Answered by nikif99 last updated on 11/May/22
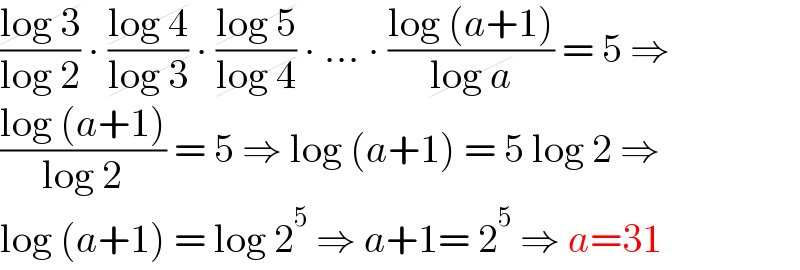
$$\frac{\cancel{\mathrm{log}\:\mathrm{3}}}{\mathrm{log}\:\mathrm{2}}\:\centerdot\:\frac{\cancel{\mathrm{log}\:\mathrm{4}}}{\cancel{\mathrm{log}\:\mathrm{3}}}\:\centerdot\:\frac{\cancel{\mathrm{log}\:\mathrm{5}}}{\cancel{\mathrm{log}\:\mathrm{4}}}\:\centerdot\:…\:\centerdot\:\frac{\mathrm{log}\:\left({a}+\mathrm{1}\right)}{\cancel{\mathrm{log}\:{a}}}\:=\:\mathrm{5}\:\Rightarrow \\ $$$$\frac{\mathrm{log}\:\left({a}+\mathrm{1}\right)}{\mathrm{log}\:\mathrm{2}}\:=\:\mathrm{5}\:\Rightarrow\:\mathrm{log}\:\left({a}+\mathrm{1}\right)\:=\:\mathrm{5}\:\mathrm{log}\:\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{log}\:\left({a}+\mathrm{1}\right)\:=\:\mathrm{log}\:\mathrm{2}^{\mathrm{5}} \:\Rightarrow\:{a}+\mathrm{1}=\:\mathrm{2}^{\mathrm{5}} \:\Rightarrow\:{a}=\mathrm{31} \\ $$
Answered by som(math1967) last updated on 11/May/22
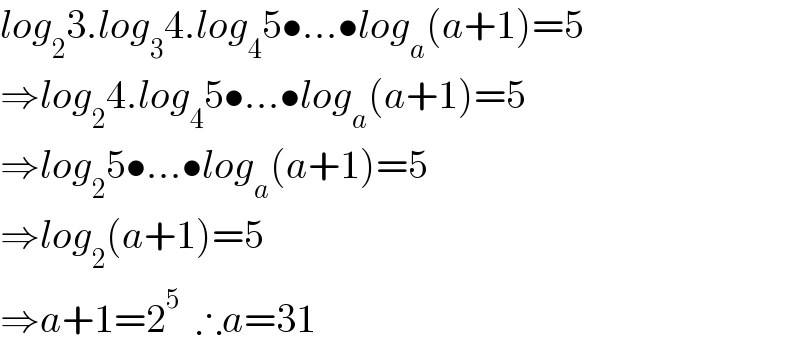
$${log}_{\mathrm{2}} \mathrm{3}.{log}_{\mathrm{3}} \mathrm{4}.{log}_{\mathrm{4}} \mathrm{5}\bullet…\bullet{log}_{{a}} \left({a}+\mathrm{1}\right)=\mathrm{5} \\ $$$$\Rightarrow{log}_{\mathrm{2}} \mathrm{4}.{log}_{\mathrm{4}} \mathrm{5}\bullet…\bullet{log}_{{a}} \left({a}+\mathrm{1}\right)=\mathrm{5} \\ $$$$\Rightarrow{log}_{\mathrm{2}} \mathrm{5}\bullet…\bullet{log}_{{a}} \left({a}+\mathrm{1}\right)=\mathrm{5} \\ $$$$\Rightarrow{log}_{\mathrm{2}} \left({a}+\mathrm{1}\right)=\mathrm{5} \\ $$$$\Rightarrow{a}+\mathrm{1}=\mathrm{2}^{\mathrm{5}} \:\:\therefore{a}=\mathrm{31} \\ $$
