Question Number 169916 by mathlove last updated on 12/May/22
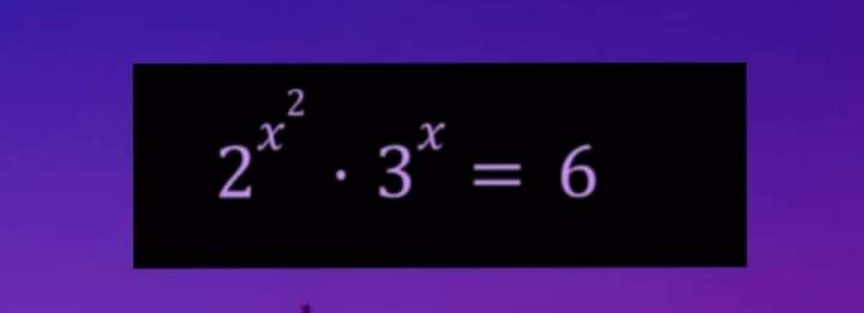
Answered by mahdipoor last updated on 12/May/22
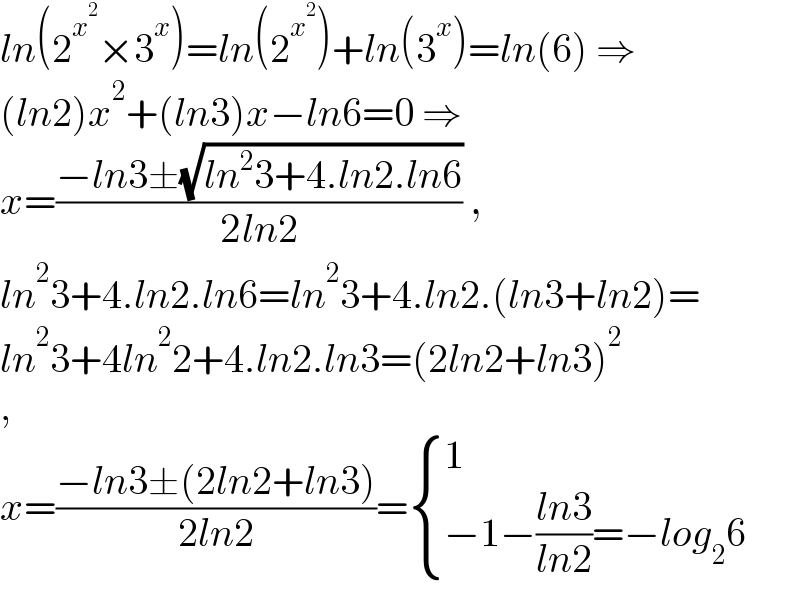
$${ln}\left(\mathrm{2}^{{x}^{\mathrm{2}} } ×\mathrm{3}^{{x}} \right)={ln}\left(\mathrm{2}^{{x}^{\mathrm{2}} } \right)+{ln}\left(\mathrm{3}^{{x}} \right)={ln}\left(\mathrm{6}\right)\:\Rightarrow \\ $$$$\left({ln}\mathrm{2}\right){x}^{\mathrm{2}} +\left({ln}\mathrm{3}\right){x}−{ln}\mathrm{6}=\mathrm{0}\:\Rightarrow \\ $$$${x}=\frac{−{ln}\mathrm{3}\pm\sqrt{{ln}^{\mathrm{2}} \mathrm{3}+\mathrm{4}.{ln}\mathrm{2}.{ln}\mathrm{6}}}{\mathrm{2}{ln}\mathrm{2}}\:, \\ $$$${ln}^{\mathrm{2}} \mathrm{3}+\mathrm{4}.{ln}\mathrm{2}.{ln}\mathrm{6}={ln}^{\mathrm{2}} \mathrm{3}+\mathrm{4}.{ln}\mathrm{2}.\left({ln}\mathrm{3}+{ln}\mathrm{2}\right)= \\ $$$${ln}^{\mathrm{2}} \mathrm{3}+\mathrm{4}{ln}^{\mathrm{2}} \mathrm{2}+\mathrm{4}.{ln}\mathrm{2}.{ln}\mathrm{3}=\left(\mathrm{2}{ln}\mathrm{2}+{ln}\mathrm{3}\right)^{\mathrm{2}} \\ $$$$, \\ $$$${x}=\frac{−{ln}\mathrm{3}\pm\left(\mathrm{2}{ln}\mathrm{2}+{ln}\mathrm{3}\right)}{\mathrm{2}{ln}\mathrm{2}}=\begin{cases}{\mathrm{1}}\\{−\mathrm{1}−\frac{{ln}\mathrm{3}}{{ln}\mathrm{2}}=−{log}_{\mathrm{2}} \mathrm{6}}\end{cases} \\ $$
