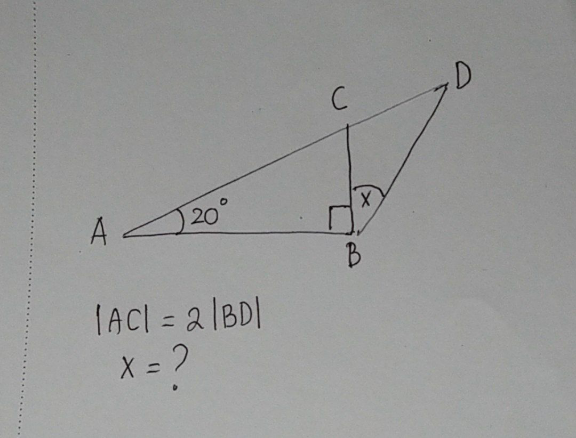
Question Number 169947 by cortano1 last updated on 13/May/22
Commented by cortano1 last updated on 13/May/22
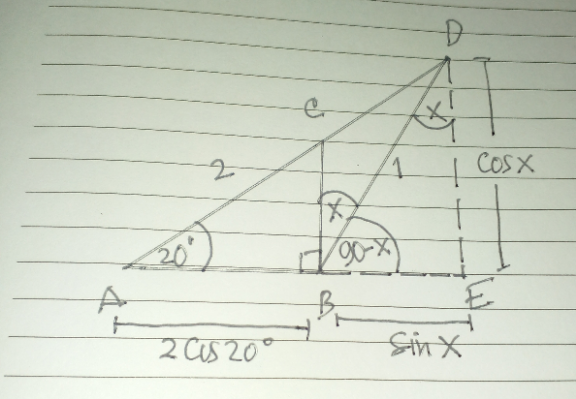
Answered by Rasheed.Sindhi last updated on 13/May/22
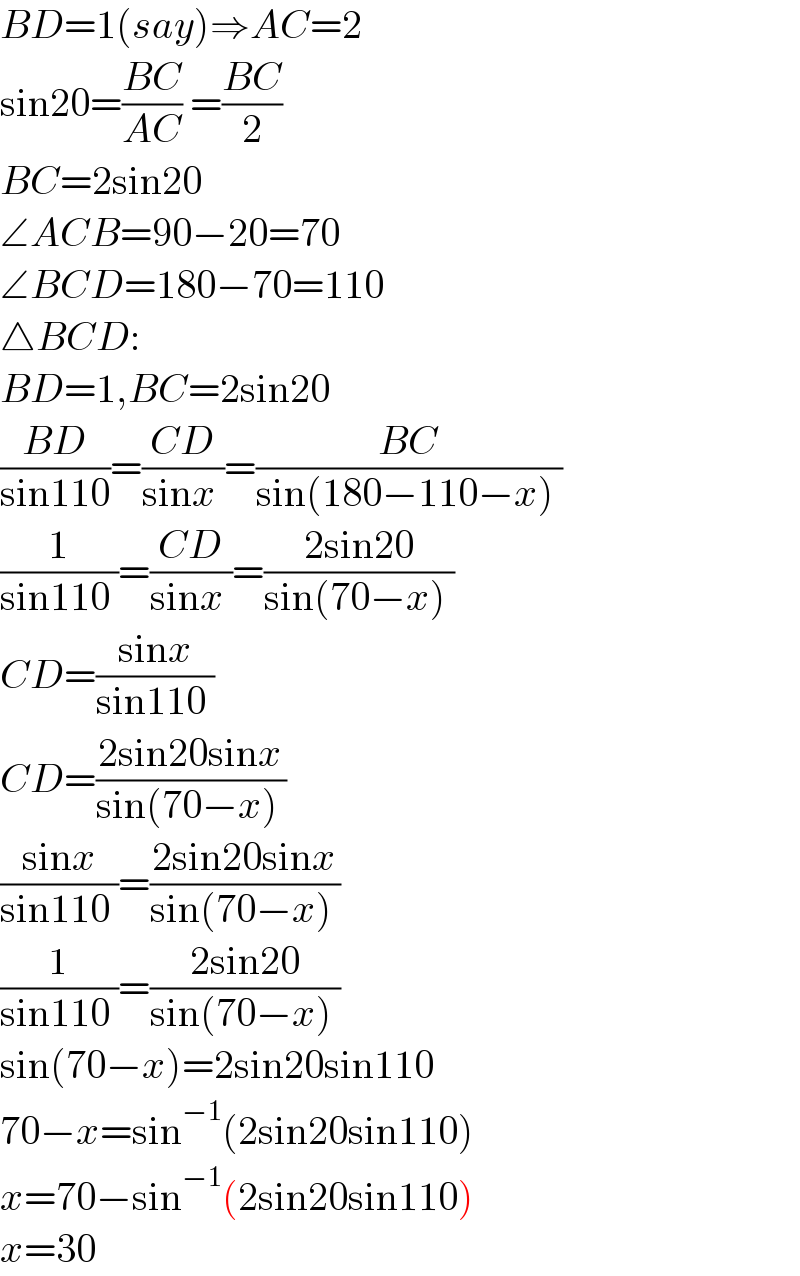
$${BD}=\mathrm{1}\left({say}\right)\Rightarrow{AC}=\mathrm{2} \\ $$$$\mathrm{sin20}=\frac{{BC}}{{AC}}\:=\frac{{BC}}{\mathrm{2}} \\ $$$${BC}=\mathrm{2sin20}\: \\ $$$$\angle{ACB}=\mathrm{90}−\mathrm{20}=\mathrm{70} \\ $$$$\angle{BCD}=\mathrm{180}−\mathrm{70}=\mathrm{110} \\ $$$$\bigtriangleup{BCD}: \\ $$$${BD}=\mathrm{1},{BC}=\mathrm{2sin20} \\ $$$$\frac{{BD}}{\mathrm{sin110}}=\frac{{CD}}{\mathrm{sin}{x}\:}=\frac{{BC}}{\mathrm{sin}\left(\mathrm{180}−\mathrm{110}−{x}\right)\:} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin110}\:}=\frac{{CD}}{\mathrm{sin}{x}\:}=\frac{\mathrm{2sin20}}{\mathrm{sin}\left(\mathrm{70}−{x}\right)\:} \\ $$$${CD}=\frac{\mathrm{sin}{x}}{\mathrm{sin110}\:} \\ $$$${CD}=\frac{\mathrm{2sin20sin}{x}}{\mathrm{sin}\left(\mathrm{70}−{x}\right)\:} \\ $$$$\frac{\mathrm{sin}{x}}{\mathrm{sin110}\:}=\frac{\mathrm{2sin20sin}{x}}{\mathrm{sin}\left(\mathrm{70}−{x}\right)\:} \\ $$$$\frac{\mathrm{1}}{\mathrm{sin110}\:}=\frac{\mathrm{2sin20}}{\mathrm{sin}\left(\mathrm{70}−{x}\right)\:} \\ $$$$\mathrm{sin}\left(\mathrm{70}−{x}\right)=\mathrm{2sin20sin110} \\ $$$$\mathrm{70}−{x}=\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{2sin20sin110}\right) \\ $$$${x}=\mathrm{70}−\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{2sin20sin110}\right) \\ $$$${x}=\mathrm{30} \\ $$
Commented by cortano1 last updated on 13/May/22
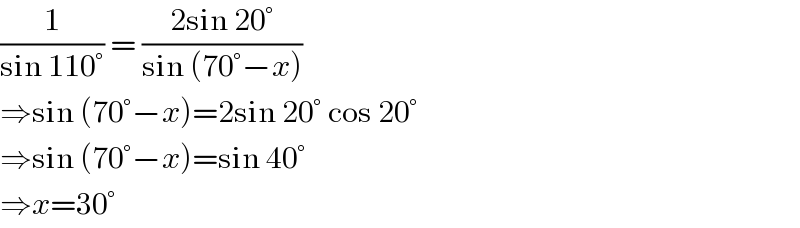
$$\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{110}°}\:=\:\frac{\mathrm{2sin}\:\mathrm{20}°}{\mathrm{sin}\:\left(\mathrm{70}°−{x}\right)} \\ $$$$\Rightarrow\mathrm{sin}\:\left(\mathrm{70}°−{x}\right)=\mathrm{2sin}\:\mathrm{20}°\:\mathrm{cos}\:\mathrm{20}° \\ $$$$\Rightarrow\mathrm{sin}\:\left(\mathrm{70}°−{x}\right)=\mathrm{sin}\:\mathrm{40}° \\ $$$$\Rightarrow{x}=\mathrm{30}° \\ $$
Answered by mr W last updated on 13/May/22
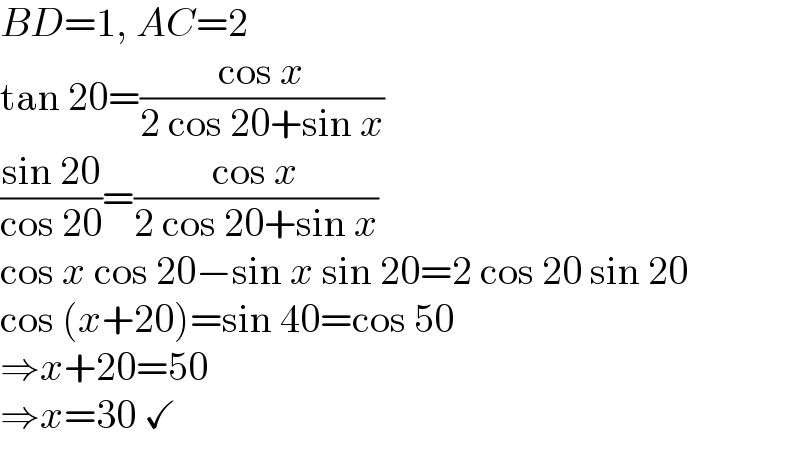
$${BD}=\mathrm{1},\:{AC}=\mathrm{2} \\ $$$$\mathrm{tan}\:\mathrm{20}=\frac{\mathrm{cos}\:{x}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{20}+\mathrm{sin}\:{x}} \\ $$$$\frac{\mathrm{sin}\:\mathrm{20}}{\mathrm{cos}\:\mathrm{20}}=\frac{\mathrm{cos}\:{x}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{20}+\mathrm{sin}\:{x}} \\ $$$$\mathrm{cos}\:{x}\:\mathrm{cos}\:\mathrm{20}−\mathrm{sin}\:{x}\:\mathrm{sin}\:\mathrm{20}=\mathrm{2}\:\mathrm{cos}\:\mathrm{20}\:\mathrm{sin}\:\mathrm{20} \\ $$$$\mathrm{cos}\:\left({x}+\mathrm{20}\right)=\mathrm{sin}\:\mathrm{40}=\mathrm{cos}\:\mathrm{50} \\ $$$$\Rightarrow{x}+\mathrm{20}=\mathrm{50} \\ $$$$\Rightarrow{x}=\mathrm{30}\:\checkmark \\ $$
