Question Number 169969 by Beginner last updated on 13/May/22

Answered by mr W last updated on 13/May/22
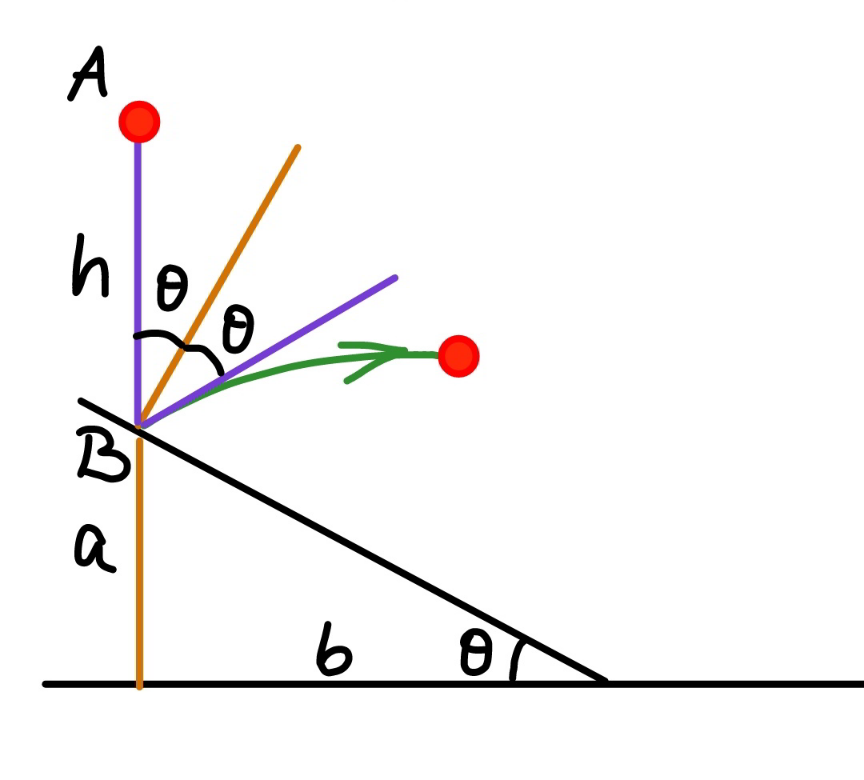
Commented by ajfour last updated on 13/May/22
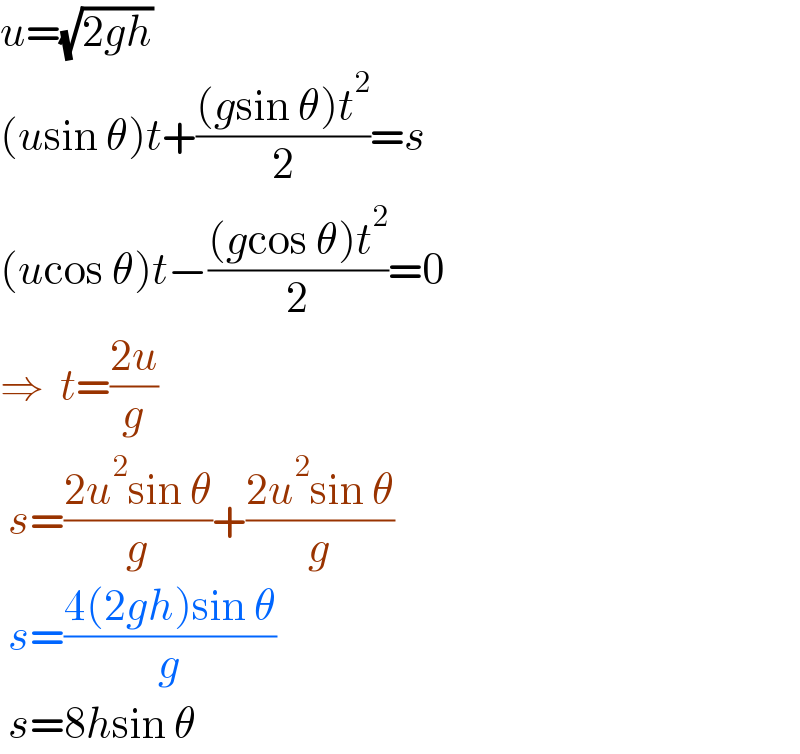
$${u}=\sqrt{\mathrm{2}{gh}} \\ $$$$\left({u}\mathrm{sin}\:\theta\right){t}+\frac{\left({g}\mathrm{sin}\:\theta\right){t}^{\mathrm{2}} }{\mathrm{2}}={s} \\ $$$$\left({u}\mathrm{cos}\:\theta\right){t}−\frac{\left({g}\mathrm{cos}\:\theta\right){t}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow\:\:{t}=\frac{\mathrm{2}{u}}{{g}} \\ $$$$\:{s}=\frac{\mathrm{2}{u}^{\mathrm{2}} \mathrm{sin}\:\theta}{{g}}+\frac{\mathrm{2}{u}^{\mathrm{2}} \mathrm{sin}\:\theta}{{g}} \\ $$$$\:{s}=\frac{\mathrm{4}\left(\mathrm{2}{gh}\right)\mathrm{sin}\:\theta}{{g}} \\ $$$$\:{s}=\mathrm{8}{h}\mathrm{sin}\:\theta \\ $$
Commented by mr W last updated on 13/May/22

$${great}\:{sir}! \\ $$
Commented by learner22 last updated on 13/May/22

$$\boldsymbol{{bravo}} \\ $$
Commented by mr W last updated on 13/May/22
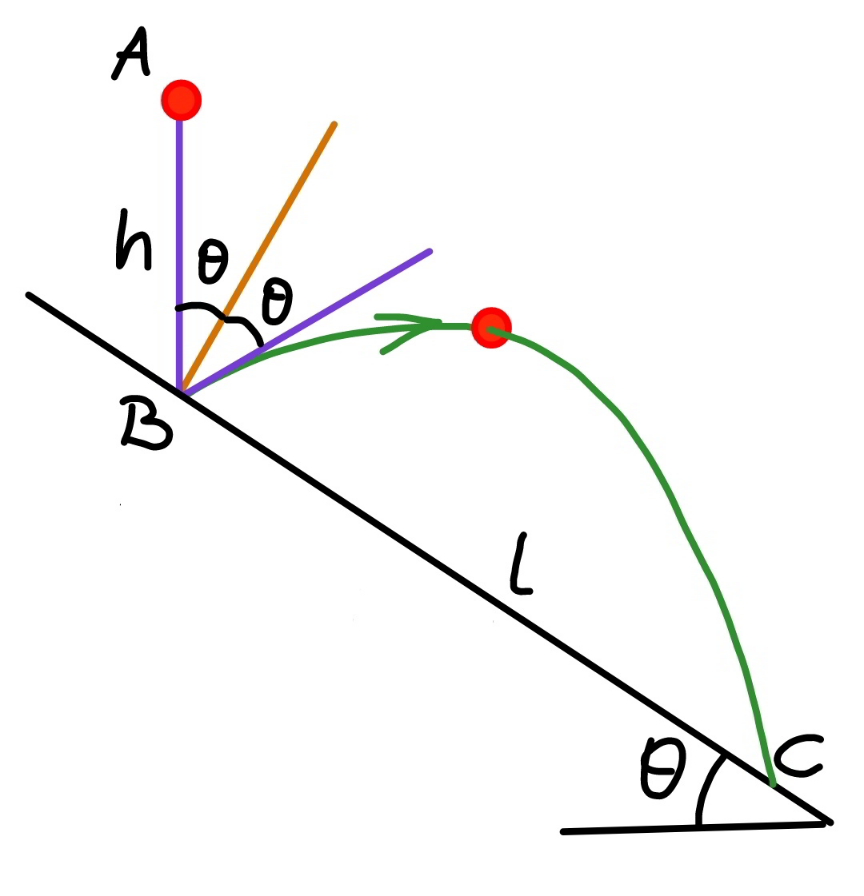
Commented by mr W last updated on 13/May/22
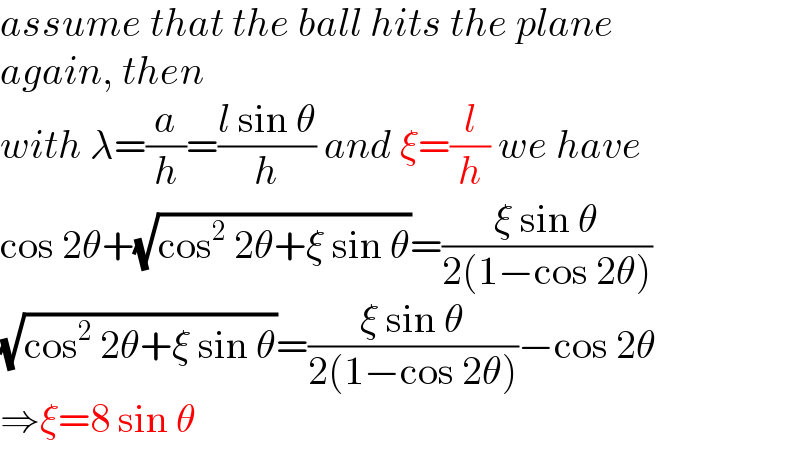
$${assume}\:{that}\:{the}\:{ball}\:{hits}\:{the}\:{plane} \\ $$$${again},\:{then} \\ $$$${with}\:\lambda=\frac{{a}}{{h}}=\frac{{l}\:\mathrm{sin}\:\theta}{{h}}\:{and}\:\xi=\frac{{l}}{{h}}\:{we}\:{have} \\ $$$$\mathrm{cos}\:\mathrm{2}\theta+\sqrt{\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}\theta+\xi\:\mathrm{sin}\:\theta}=\frac{\xi\:\mathrm{sin}\:\theta}{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta\right)} \\ $$$$\sqrt{\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}\theta+\xi\:\mathrm{sin}\:\theta}=\frac{\xi\:\mathrm{sin}\:\theta}{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta\right)}−\mathrm{cos}\:\mathrm{2}\theta \\ $$$$\Rightarrow\xi=\mathrm{8}\:\mathrm{sin}\:\theta \\ $$
Commented by mr W last updated on 13/May/22

$${say}\:{impact}\:{point}\:{B}\:{is}\:{a}\:{above}\:{the} \\ $$$${ground}. \\ $$$${speed}\:{at}\:{point}\:{B}: \\ $$$${v}=\sqrt{\mathrm{2}{gh}} \\ $$$${upon}\:{point}\:{B}: \\ $$$${x}={v}\:\mathrm{sin}\:\mathrm{2}\theta\:{t} \\ $$$${y}={a}+{v}\:\mathrm{cos}\:\mathrm{2}\theta\:{t}−\frac{{gt}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${y}={a}+{v}\:\mathrm{cos}\:\mathrm{2}\theta×\frac{{x}}{{v}\:\mathrm{sin}\:\mathrm{2}\theta}−\frac{{g}}{\mathrm{2}}×\left(\frac{{x}}{{v}\:\mathrm{sin}\:\mathrm{2}\theta}\right)^{\mathrm{2}} \\ $$$${y}={a}+\frac{{x}}{\mathrm{tan}\:\mathrm{2}\theta}−\frac{{gx}^{\mathrm{2}} }{\mathrm{2}{v}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}\theta} \\ $$$$\Rightarrow{y}={a}+\frac{{x}}{\mathrm{tan}\:\mathrm{2}\theta}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}{h}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}\theta} \\ $$$${at}\:{y}=\mathrm{0}: \\ $$$${a}+\frac{{x}}{\mathrm{tan}\:\mathrm{2}\theta}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}{h}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}\theta}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\frac{\mathrm{4}{h}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}\theta{x}}{\mathrm{tan}\:\mathrm{2}\theta}−\mathrm{4}{ah}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}\theta=\mathrm{0} \\ $$$${x}=\frac{\mathrm{2}{h}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}\theta}{\mathrm{tan}\:\mathrm{2}\theta}+\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta\sqrt{{h}\left({h}\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}\theta+{a}\right)} \\ $$$${such}\:{that}\:{the}\:{ball}\:{hits}\:{the}\:{plane}\:{again}, \\ $$$${x}=\frac{\mathrm{2}{h}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}\theta}{\mathrm{tan}\:\mathrm{2}\theta}+\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta\sqrt{{h}\left({h}\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}\theta+{a}\right)}\leqslant{b}=\frac{{a}}{\mathrm{tan}\:\theta} \\ $$$$\frac{\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}\theta}{\mathrm{tan}\:\mathrm{2}\theta}+\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta\sqrt{\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}\theta+\frac{{a}}{{h}}}\leqslant\frac{{a}}{{h}\:\mathrm{tan}\:\theta} \\ $$$${let}\:\lambda=\frac{{a}}{{h}} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{2}\theta+\sqrt{\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}\theta+\lambda}\leqslant\frac{\lambda}{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta\right)} \\ $$$${example}:\:\theta=\mathrm{30}° \\ $$$$\lambda=\mathrm{2}.\mathrm{2873} \\ $$$${i}.{e}.\:{when}\:\frac{{a}}{{h}}\geqslant\mathrm{2}.\mathrm{2873},\:{the}\:{ball}\:{will} \\ $$$${hit}\:{the}\:{plane}\:{again}\:{after}\:{the}\:{impact}. \\ $$
Commented by Tawa11 last updated on 14/May/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
