Question Number 169973 by Best1 last updated on 13/May/22
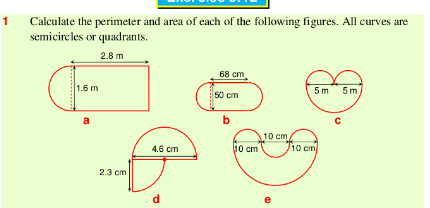
Answered by alephzero last updated on 13/May/22
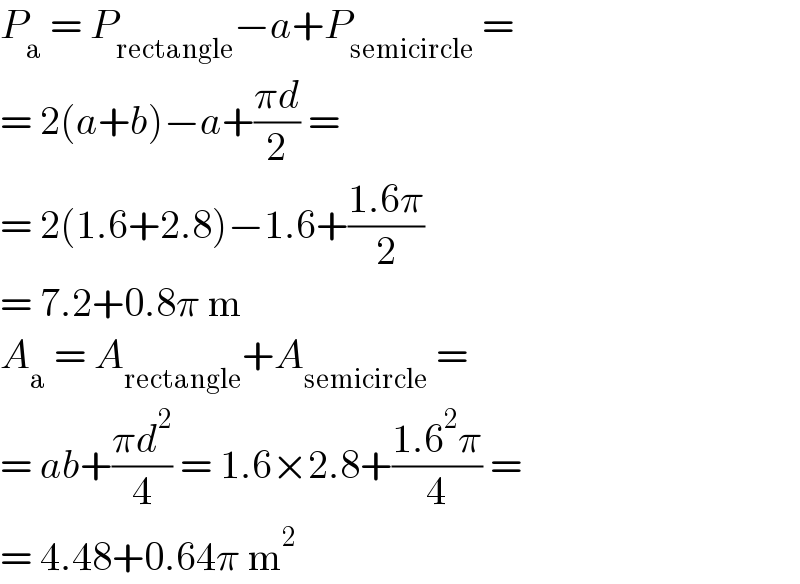
$${P}_{\mathrm{a}} \:=\:{P}_{\mathrm{rectangle}} −{a}+{P}_{\mathrm{semicircle}} \:= \\ $$$$=\:\mathrm{2}\left({a}+{b}\right)−{a}+\frac{\pi{d}}{\mathrm{2}}\:= \\ $$$$=\:\mathrm{2}\left(\mathrm{1}.\mathrm{6}+\mathrm{2}.\mathrm{8}\right)−\mathrm{1}.\mathrm{6}+\frac{\mathrm{1}.\mathrm{6}\pi}{\mathrm{2}} \\ $$$$=\:\mathrm{7}.\mathrm{2}+\mathrm{0}.\mathrm{8}\pi\:\mathrm{m} \\ $$$${A}_{\mathrm{a}} \:=\:{A}_{\mathrm{rectangle}} +{A}_{\mathrm{semicircle}} \:= \\ $$$$=\:{ab}+\frac{\pi{d}^{\mathrm{2}} }{\mathrm{4}}\:=\:\mathrm{1}.\mathrm{6}×\mathrm{2}.\mathrm{8}+\frac{\mathrm{1}.\mathrm{6}^{\mathrm{2}} \pi}{\mathrm{4}}\:= \\ $$$$=\:\mathrm{4}.\mathrm{48}+\mathrm{0}.\mathrm{64}\pi\:\mathrm{m}^{\mathrm{2}} \\ $$
Commented by Best1 last updated on 13/May/22

$${what}\:{abou}\:{c}\:{d}\:{e}? \\ $$
