Question Number 169977 by infinityaction last updated on 13/May/22
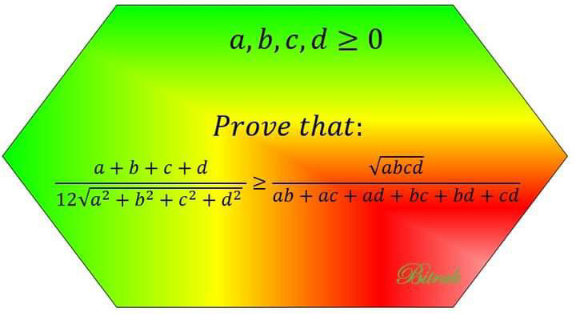
Answered by ajfour last updated on 13/May/22
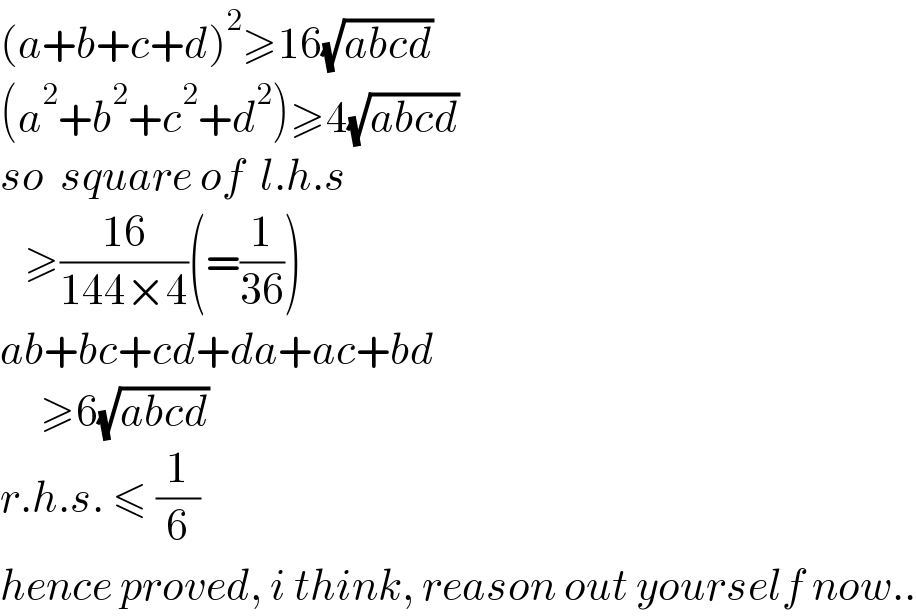
$$\left({a}+{b}+{c}+{d}\right)^{\mathrm{2}} \geqslant\mathrm{16}\sqrt{{abcd}} \\ $$$$\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)\geqslant\mathrm{4}\sqrt{{abcd}} \\ $$$${so}\:\:{square}\:{of}\:\:{l}.{h}.{s} \\ $$$$\:\:\:\geqslant\frac{\mathrm{16}}{\mathrm{144}×\mathrm{4}}\left(=\frac{\mathrm{1}}{\mathrm{36}}\right) \\ $$$${ab}+{bc}+{cd}+{da}+{ac}+{bd} \\ $$$$\:\:\:\:\:\geqslant\mathrm{6}\sqrt{{abcd}} \\ $$$${r}.{h}.{s}.\:\leqslant\:\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${hence}\:{proved},\:{i}\:{think},\:{reason}\:{out}\:{yourself}\:{now}.. \\ $$
