Question Number 170010 by mr W last updated on 13/May/22
Commented by mr W last updated on 13/May/22
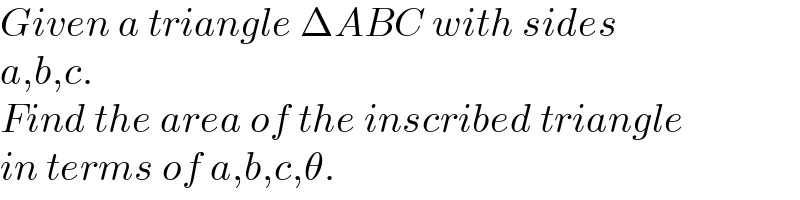
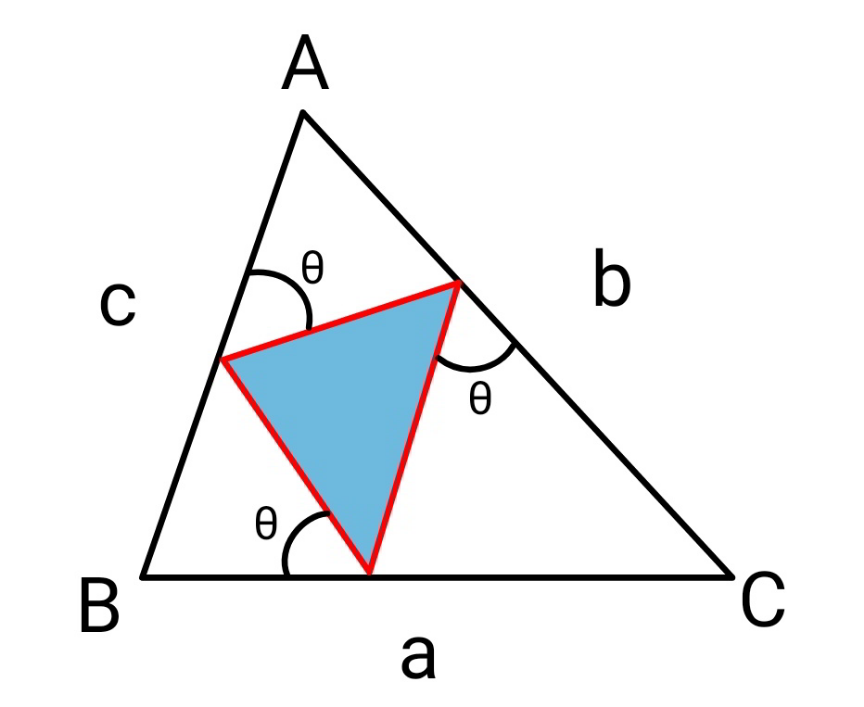
$${Given}\:{a}\:{triangle}\:\Delta{ABC}\:{with}\:{sides} \\ $$$${a},{b},{c}. \\ $$$${Find}\:{the}\:{area}\:{of}\:{the}\:{inscribed}\:{triangle} \\ $$$${in}\:{terms}\:{of}\:{a},{b},{c},\theta. \\ $$
Answered by mr W last updated on 15/May/22
Commented by mr W last updated on 15/May/22
![we can see that ΔQRP∼ΔABC ⇒(p/c)=(q/a)=(r/b)=k, say ((BP)/(sin (B+θ)))=((RP)/(sin B)) ⇒BP=((ka sin (B+θ))/(sin B)) ((PC)/(sin θ))=((PQ)/(sin C)) ⇒PC=((kb sin θ)/(sin C)) a=((ka sin (B+θ))/(sin B))+((kb sin θ)/(sin C)) ⇒a×((sin B−k sin (B+θ))/(sin B))=((kb sin θ)/(sin C)) (i) similarly ⇒b×((sin C−k sin (C+θ))/(sin C))=((kc sin θ)/(sin A)) (ii) ⇒c×((sin A−k sin (A+θ))/(sin A))=((ka sin θ)/(sin B)) (iii) (i)×(ii)×(iii): [sin A−k sin (A+θ)][sin B−k sin (B+θ)][sin C−k sin (C+θ)]=sin^3 θ k^3 [sin^3 θ+sin (A+θ) sin (B+θ) sin (C+θ)]k^3 −[sin A sin (B+θ) sin (C+θ)+sin B sin (C+θ) sin (A+θ)+sin C sin (A+θ) sin (B+θ)]k^2 +[sin A sin B sin (C+θ)+sin (A+θ) sin B sin C+sin A sin B sin (C+θ)]k −sin A sin B sin C=0 sin^3 θ+sin (A+θ) sin (B+θ) sin (C+θ) =sin^3 θ+(sin A cos θ+cos A sin θ)(sin B cos θ+cos B sin θ)(sin C cos θ+cos C sin θ) =sin^3 θ+[sin A sin B−cos C sin^2 θ+sin C sin θ cos θ](sin C cos θ+cos C sin θ) =sin^3 θ+sin A sin B sin C cos θ− sin^3 θ+(cos A cos B cos C+1)sin θ =sin A sin B sin C cos θ+(cos A cos B cos C+1) sin θ sin A sin (B+θ) sin (C+θ) =sin A (sin B cos θ+cos B sin θ)(sin C cos θ+cos C sin θ) =sin A (sin B sin C cos^2 θ+sin A sin θ cos θ+cos B cos C sin^2 θ) =sin A sin B sin C cos^2 θ+sin^2 A sin θ cos θ+(1/4)(sin 2A+sin 2B− sin 2C) sin^2 θ Σ=3 sin A sin B sin C cos^2 θ+(sin^2 A+sin^2 B+sin^2 C)sin θ cos θ +(3/4)(sin 2A+sin 2B+ sin 2C) sin^2 θ−(1/2)(sin 2A+sin 2B+sin 2C) sin^2 θ =sin A sin B sin C (cos 2θ+2)+(cos A cos B cos C+1) sin 2θ sin A sin B sin (C+θ) sin A sin B (sin C cos θ+cos C sin θ) sin A sin B sin C cos θ+(1/2)(sin^2 A+sin^2 B+sin^2 C)sin θ−sin^2 C sin θ Σ=3 sin A sin B sin C cos θ+(cos A cos B cos C+1) sin θ {sin A sin B sin C cos θ+(cos A cos B cos C+1) sin θ}k^3 −{sin A sin B sin C (cos 2θ+2)+(cos A cos B cos C+1) sin 2θ}k^2 +{3 sin A sin B sin C cos θ+(cos A cos B cos C+1) sin θ}k −sin A sin B sin C=0 or let λ=((cos A cos B cos C+1)/(sin A sin B sin C))=((a^2 +b^2 +c^2 )/(4Δ_(ABC) )) (cos 𝛉+𝛌 sin 𝛉)k^3 −(2+cos 2𝛉+𝛌 sin 2𝛉)k^2 +(3 cos 𝛉+𝛌 sin 𝛉)k−1=0 ⇒ determinant (((k=(1/(cos 𝛉+𝛌 sin 𝛉))))) (wow! i didn′t expect that the root of this complicated cubic equation is so brief!) Δ_(PQR) =k^2 Δ_(ABC) 𝚫_(PQR) =(𝚫_(ABC) /((cos 𝛉+𝛌 sin 𝛉)^2 )) special case: θ=(π/2) ⇒k=(1/λ)=((sin A sin B sin C)/(cos A cos B cos C+1)) this is the same as we get in Q169815.](https://www.tinkutara.com/question/Q170061.png)
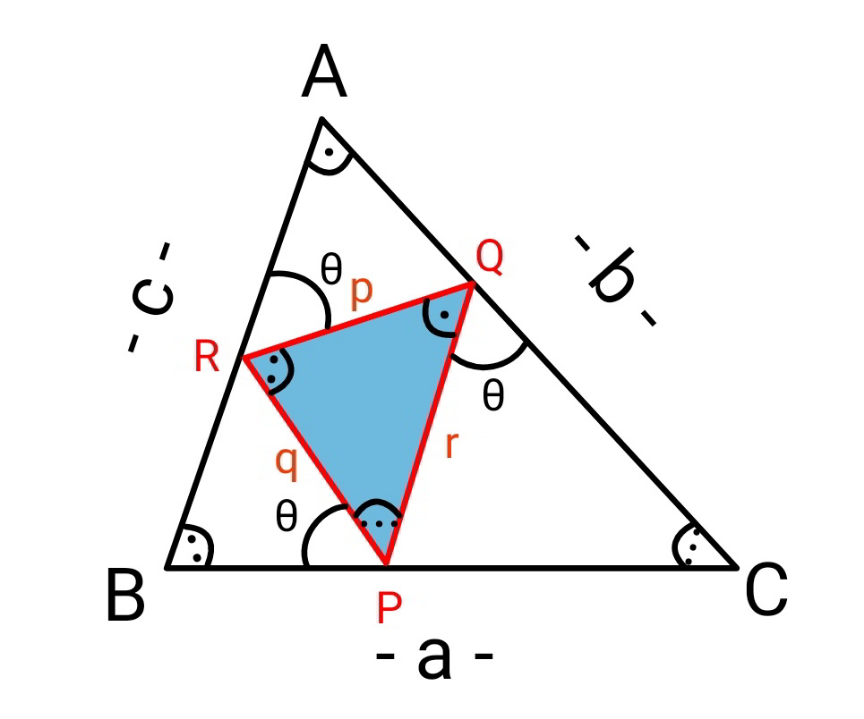
$${we}\:{can}\:{see}\:{that} \\ $$$$\Delta{QRP}\sim\Delta{ABC} \\ $$$$\Rightarrow\frac{{p}}{{c}}=\frac{{q}}{{a}}=\frac{{r}}{{b}}={k},\:{say} \\ $$$$\frac{{BP}}{\mathrm{sin}\:\left({B}+\theta\right)}=\frac{{RP}}{\mathrm{sin}\:{B}} \\ $$$$\Rightarrow{BP}=\frac{{ka}\:\mathrm{sin}\:\left({B}+\theta\right)}{\mathrm{sin}\:{B}} \\ $$$$\frac{{PC}}{\mathrm{sin}\:\theta}=\frac{{PQ}}{\mathrm{sin}\:{C}} \\ $$$$\Rightarrow{PC}=\frac{{kb}\:\mathrm{sin}\:\theta}{\mathrm{sin}\:{C}} \\ $$$${a}=\frac{{ka}\:\mathrm{sin}\:\left({B}+\theta\right)}{\mathrm{sin}\:{B}}+\frac{{kb}\:\mathrm{sin}\:\theta}{\mathrm{sin}\:{C}} \\ $$$$\Rightarrow{a}×\frac{\mathrm{sin}\:{B}−{k}\:\mathrm{sin}\:\left({B}+\theta\right)}{\mathrm{sin}\:{B}}=\frac{{kb}\:\mathrm{sin}\:\theta}{\mathrm{sin}\:{C}}\:\:\:\left({i}\right) \\ $$$${similarly} \\ $$$$\Rightarrow{b}×\frac{\mathrm{sin}\:{C}−{k}\:\mathrm{sin}\:\left({C}+\theta\right)}{\mathrm{sin}\:{C}}=\frac{{kc}\:\mathrm{sin}\:\theta}{\mathrm{sin}\:{A}}\:\:\:\left({ii}\right) \\ $$$$\Rightarrow{c}×\frac{\mathrm{sin}\:{A}−{k}\:\mathrm{sin}\:\left({A}+\theta\right)}{\mathrm{sin}\:{A}}=\frac{{ka}\:\mathrm{sin}\:\theta}{\mathrm{sin}\:{B}}\:\:\:\left({iii}\right) \\ $$$$\left({i}\right)×\left({ii}\right)×\left({iii}\right): \\ $$$$\left[\mathrm{sin}\:{A}−{k}\:\mathrm{sin}\:\left({A}+\theta\right)\right]\left[\mathrm{sin}\:{B}−{k}\:\mathrm{sin}\:\left({B}+\theta\right)\right]\left[\mathrm{sin}\:{C}−{k}\:\mathrm{sin}\:\left({C}+\theta\right)\right]=\mathrm{sin}^{\mathrm{3}} \:\theta\:{k}^{\mathrm{3}} \\ $$$$ \\ $$$$\left[\mathrm{sin}^{\mathrm{3}} \:\theta+\mathrm{sin}\:\left({A}+\theta\right)\:\mathrm{sin}\:\left({B}+\theta\right)\:\mathrm{sin}\:\left({C}+\theta\right)\right]{k}^{\mathrm{3}} \\ $$$$−\left[\mathrm{sin}\:{A}\:\mathrm{sin}\:\left({B}+\theta\right)\:\mathrm{sin}\:\left({C}+\theta\right)+\mathrm{sin}\:{B}\:\mathrm{sin}\:\left({C}+\theta\right)\:\mathrm{sin}\:\left({A}+\theta\right)+\mathrm{sin}\:{C}\:\mathrm{sin}\:\left({A}+\theta\right)\:\mathrm{sin}\:\left({B}+\theta\right)\right]{k}^{\mathrm{2}} \\ $$$$+\left[\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:\left({C}+\theta\right)+\mathrm{sin}\:\left({A}+\theta\right)\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}+\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:\left({C}+\theta\right)\right]{k} \\ $$$$−\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}=\mathrm{0} \\ $$$$ \\ $$$$\mathrm{sin}^{\mathrm{3}} \:\theta+\mathrm{sin}\:\left({A}+\theta\right)\:\mathrm{sin}\:\left({B}+\theta\right)\:\mathrm{sin}\:\left({C}+\theta\right) \\ $$$$=\mathrm{sin}^{\mathrm{3}} \:\theta+\left(\mathrm{sin}\:{A}\:\mathrm{cos}\:\theta+\mathrm{cos}\:{A}\:\mathrm{sin}\:\theta\right)\left(\mathrm{sin}\:{B}\:\mathrm{cos}\:\theta+\mathrm{cos}\:{B}\:\mathrm{sin}\:\theta\right)\left(\mathrm{sin}\:{C}\:\mathrm{cos}\:\theta+\mathrm{cos}\:{C}\:\mathrm{sin}\:\theta\right) \\ $$$$=\mathrm{sin}^{\mathrm{3}} \:\theta+\left[\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}−\mathrm{cos}\:{C}\:\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{sin}\:{C}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\right]\left(\mathrm{sin}\:{C}\:\mathrm{cos}\:\theta+\mathrm{cos}\:{C}\:\mathrm{sin}\:\theta\right) \\ $$$$=\mathrm{sin}^{\mathrm{3}} \:\theta+\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}\:\mathrm{cos}\:\theta−\:\mathrm{sin}^{\mathrm{3}} \:\:\theta+\left(\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}+\mathrm{1}\right)\mathrm{sin}\:\theta\: \\ $$$$=\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}\:\mathrm{cos}\:\theta+\left(\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}+\mathrm{1}\right)\:\mathrm{sin}\:\theta\: \\ $$$$ \\ $$$$\mathrm{sin}\:{A}\:\mathrm{sin}\:\left({B}+\theta\right)\:\mathrm{sin}\:\left({C}+\theta\right) \\ $$$$=\mathrm{sin}\:{A}\:\left(\mathrm{sin}\:{B}\:\mathrm{cos}\:\theta+\mathrm{cos}\:{B}\:\mathrm{sin}\:\theta\right)\left(\mathrm{sin}\:{C}\:\mathrm{cos}\:\theta+\mathrm{cos}\:{C}\:\mathrm{sin}\:\theta\right) \\ $$$$=\mathrm{sin}\:{A}\:\left(\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}\:\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{sin}\:{A}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta+\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}\:\mathrm{sin}^{\mathrm{2}} \:\theta\right) \\ $$$$=\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}\:\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{sin}^{\mathrm{2}} \:{A}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{sin}\:\mathrm{2}{A}+\mathrm{sin}\:\mathrm{2}{B}−\:\mathrm{sin}\:\mathrm{2}{C}\right)\:\mathrm{sin}^{\mathrm{2}} \:\theta \\ $$$$\Sigma=\mathrm{3}\:\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}\:\mathrm{cos}^{\mathrm{2}} \:\theta+\left(\mathrm{sin}^{\mathrm{2}} \:{A}+\mathrm{sin}^{\mathrm{2}} \:{B}+\mathrm{sin}^{\mathrm{2}} \:{C}\right)\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta \\ $$$$\:\:\:+\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{sin}\:\mathrm{2}{A}+\mathrm{sin}\:\mathrm{2}{B}+\:\mathrm{sin}\:\mathrm{2}{C}\right)\:\mathrm{sin}^{\mathrm{2}} \:\theta−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{sin}\:\mathrm{2}{A}+\mathrm{sin}\:\mathrm{2}{B}+\mathrm{sin}\:\mathrm{2}{C}\right)\:\mathrm{sin}^{\mathrm{2}} \:\theta \\ $$$$=\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}\:\left(\mathrm{cos}\:\mathrm{2}\theta+\mathrm{2}\right)+\left(\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:\:{C}+\mathrm{1}\right)\:\mathrm{sin}\:\mathrm{2}\theta \\ $$$$ \\ $$$$\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:\left({C}+\theta\right) \\ $$$$\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\left(\mathrm{sin}\:{C}\:\mathrm{cos}\:\theta+\mathrm{cos}\:{C}\:\mathrm{sin}\:\theta\right) \\ $$$$\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}\:\mathrm{cos}\:\theta+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{sin}^{\mathrm{2}} \:{A}+\mathrm{sin}^{\mathrm{2}} \:{B}+\mathrm{sin}^{\mathrm{2}} \:{C}\right)\mathrm{sin}\:\theta−\mathrm{sin}^{\mathrm{2}} \:{C}\:\mathrm{sin}\:\theta \\ $$$$\Sigma=\mathrm{3}\:\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}\:\mathrm{cos}\:\theta+\left(\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}+\mathrm{1}\right)\:\mathrm{sin}\:\theta \\ $$$$ \\ $$$$\left\{\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}\:\mathrm{cos}\:\theta+\left(\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}+\mathrm{1}\right)\:\mathrm{sin}\:\theta\right\}{k}^{\mathrm{3}} \: \\ $$$$−\left\{\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}\:\left(\mathrm{cos}\:\mathrm{2}\theta+\mathrm{2}\right)+\left(\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:\:{C}+\mathrm{1}\right)\:\mathrm{sin}\:\mathrm{2}\theta\right\}{k}^{\mathrm{2}} \\ $$$$+\left\{\mathrm{3}\:\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}\:\mathrm{cos}\:\theta+\left(\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}+\mathrm{1}\right)\:\mathrm{sin}\:\theta\right\}{k} \\ $$$$−\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}=\mathrm{0} \\ $$$${or} \\ $$$${let}\:\lambda=\frac{\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}+\mathrm{1}}{\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{4}\Delta_{{ABC}} } \\ $$$$\left(\boldsymbol{\mathrm{cos}}\:\boldsymbol{\theta}+\boldsymbol{\lambda}\:\boldsymbol{\mathrm{sin}}\:\boldsymbol{\theta}\right)\boldsymbol{{k}}^{\mathrm{3}} −\left(\mathrm{2}+\boldsymbol{\mathrm{cos}}\:\mathrm{2}\boldsymbol{\theta}+\boldsymbol{\lambda}\:\boldsymbol{\mathrm{sin}}\:\mathrm{2}\boldsymbol{\theta}\right){k}^{\mathrm{2}} \\ $$$$+\left(\mathrm{3}\:\boldsymbol{\mathrm{cos}}\:\boldsymbol{\theta}+\boldsymbol{\lambda}\:\boldsymbol{\mathrm{sin}}\:\boldsymbol{\theta}\right)\boldsymbol{{k}}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\begin{array}{|c|}{\boldsymbol{{k}}=\frac{\mathrm{1}}{\boldsymbol{\mathrm{cos}}\:\boldsymbol{\theta}+\boldsymbol{\lambda}\:\boldsymbol{\mathrm{sin}}\:\boldsymbol{\theta}}}\\\hline\end{array} \\ $$$$\left({wow}!\:{i}\:{didn}'{t}\:{expect}\:{that}\:{the}\:{root}\:\right. \\ $$$${of}\:{this}\:{complicated}\:{cubic}\:{equation}\:{is}\: \\ $$$$\left.{so}\:{brief}!\right) \\ $$$$ \\ $$$$\Delta_{{PQR}} ={k}^{\mathrm{2}} \Delta_{{ABC}} \\ $$$$\boldsymbol{\Delta}_{\boldsymbol{{PQR}}} =\frac{\boldsymbol{\Delta}_{\boldsymbol{{ABC}}} }{\left(\boldsymbol{\mathrm{cos}}\:\boldsymbol{\theta}+\boldsymbol{\lambda}\:\boldsymbol{\mathrm{sin}}\:\boldsymbol{\theta}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$${special}\:{case}:\:\theta=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow{k}=\frac{\mathrm{1}}{\lambda}=\frac{\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}}{\mathrm{cos}\:{A}\:\mathrm{cos}\:{B}\:\mathrm{cos}\:{C}+\mathrm{1}} \\ $$$${this}\:{is}\:{the}\:{same}\:{as}\:{we}\:{get}\:{in}\:{Q}\mathrm{169815}. \\ $$
Commented by Tawa11 last updated on 08/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
