Question Number 170025 by 0731619 last updated on 14/May/22
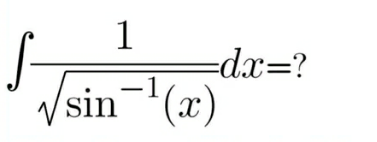
Answered by Mathspace last updated on 14/May/22
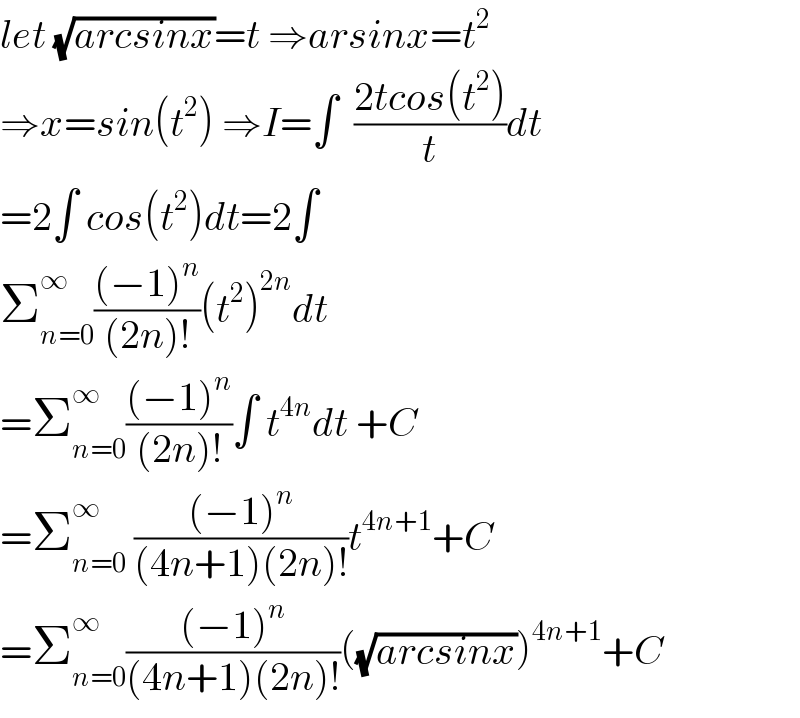
$${let}\:\sqrt{{arcsinx}}={t}\:\Rightarrow{arsinx}={t}^{\mathrm{2}} \\ $$$$\Rightarrow{x}={sin}\left({t}^{\mathrm{2}} \right)\:\Rightarrow{I}=\int\:\:\frac{\mathrm{2}{tcos}\left({t}^{\mathrm{2}} \right)}{{t}}{dt} \\ $$$$=\mathrm{2}\int\:{cos}\left({t}^{\mathrm{2}} \right){dt}=\mathrm{2}\int \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}\right)!}\left({t}^{\mathrm{2}} \right)^{\mathrm{2}{n}} {dt} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}\right)!}\int\:{t}^{\mathrm{4}{n}} {dt}\:+{C} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{4}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}\right)!}{t}^{\mathrm{4}{n}+\mathrm{1}} +{C} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{4}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}\right)!}\left(\sqrt{{arcsinx}}\right)^{\mathrm{4}{n}+\mathrm{1}} +{C} \\ $$
Commented by Mathspace last updated on 14/May/22
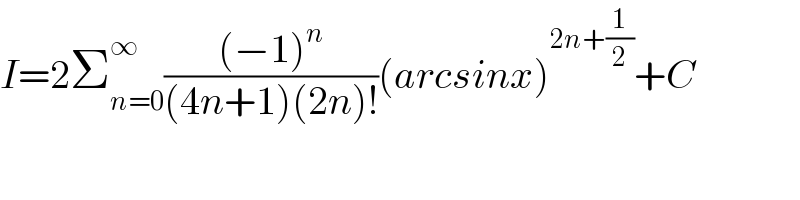
$${I}=\mathrm{2}\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{4}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}\right)!}\left({arcsinx}\right)^{\mathrm{2}{n}+\frac{\mathrm{1}}{\mathrm{2}}} +{C} \\ $$
