Question Number 170053 by mathlove last updated on 15/May/22
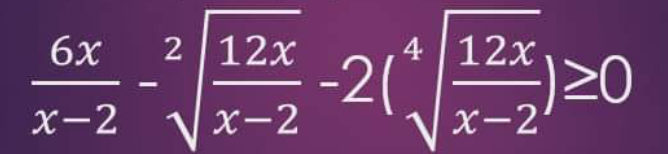
Answered by greougoury555 last updated on 15/May/22
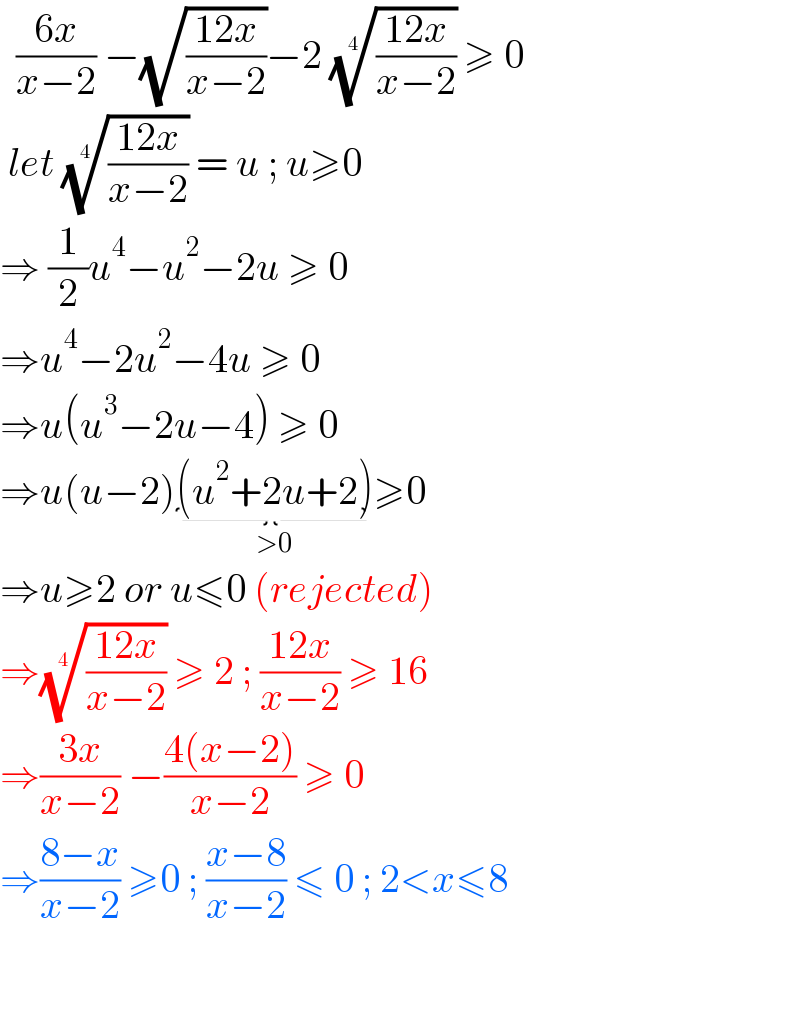
$$\:\:\frac{\mathrm{6}{x}}{{x}−\mathrm{2}}\:−\sqrt{\frac{\mathrm{12}{x}}{{x}−\mathrm{2}}}−\mathrm{2}\:\sqrt[{\mathrm{4}}]{\frac{\mathrm{12}{x}}{{x}−\mathrm{2}}}\:\geqslant\:\mathrm{0} \\ $$$$\:{let}\:\sqrt[{\mathrm{4}}]{\frac{\mathrm{12}{x}}{{x}−\mathrm{2}}}\:=\:{u}\:;\:{u}\geqslant\mathrm{0} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}{u}^{\mathrm{4}} −{u}^{\mathrm{2}} −\mathrm{2}{u}\:\geqslant\:\mathrm{0} \\ $$$$\Rightarrow{u}^{\mathrm{4}} −\mathrm{2}{u}^{\mathrm{2}} −\mathrm{4}{u}\:\geqslant\:\mathrm{0} \\ $$$$\Rightarrow{u}\left({u}^{\mathrm{3}} −\mathrm{2}{u}−\mathrm{4}\right)\:\geqslant\:\mathrm{0} \\ $$$$\Rightarrow{u}\left({u}−\mathrm{2}\right)\underset{>\mathrm{0}} {\underbrace{\left({u}^{\mathrm{2}} +\mathrm{2}{u}+\mathrm{2}\right)}}\geqslant\mathrm{0} \\ $$$$\Rightarrow{u}\geqslant\mathrm{2}\:{or}\:{u}\leqslant\mathrm{0}\:\left({rejected}\right) \\ $$$$\Rightarrow\sqrt[{\mathrm{4}}]{\frac{\mathrm{12}{x}}{{x}−\mathrm{2}}}\:\geqslant\:\mathrm{2}\:;\:\frac{\mathrm{12}{x}}{{x}−\mathrm{2}}\:\geqslant\:\mathrm{16} \\ $$$$\Rightarrow\frac{\mathrm{3}{x}}{{x}−\mathrm{2}}\:−\frac{\mathrm{4}\left({x}−\mathrm{2}\right)}{{x}−\mathrm{2}}\:\geqslant\:\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{8}−{x}}{{x}−\mathrm{2}}\:\geqslant\mathrm{0}\:;\:\frac{{x}−\mathrm{8}}{{x}−\mathrm{2}}\:\leqslant\:\mathrm{0}\:;\:\mathrm{2}<{x}\leqslant\mathrm{8} \\ $$$$\: \\ $$$$ \\ $$
