Question Number 170126 by daus last updated on 17/May/22

Commented by daus last updated on 17/May/22
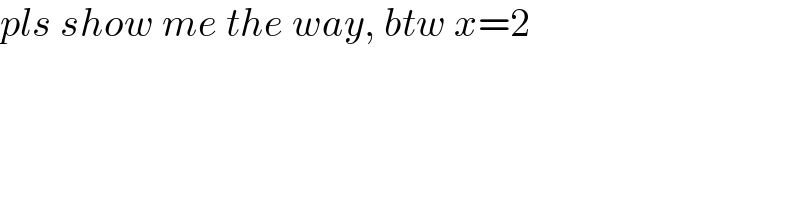
$${pls}\:{show}\:{me}\:{the}\:{way},\:{btw}\:{x}=\mathrm{2} \\ $$
Commented by mr W last updated on 17/May/22
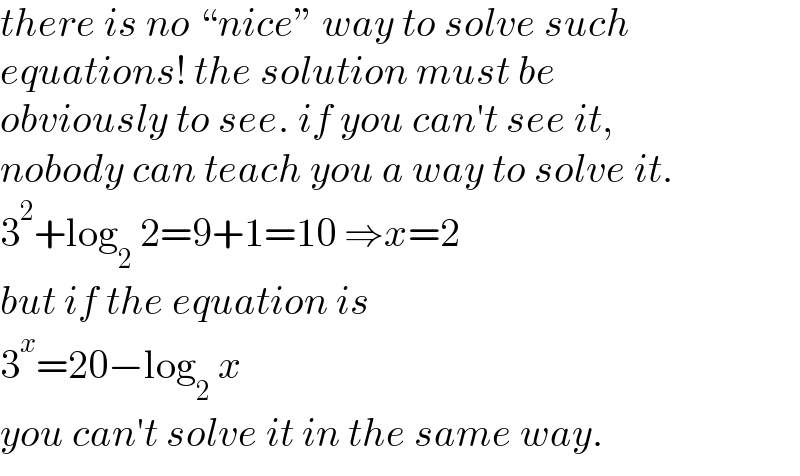
$${there}\:{is}\:{no}\:“{nice}''\:{way}\:{to}\:{solve}\:{such} \\ $$$${equations}!\:{the}\:{solution}\:{must}\:{be}\: \\ $$$${obviously}\:{to}\:{see}.\:{if}\:{you}\:{can}'{t}\:{see}\:{it},\: \\ $$$${nobody}\:{can}\:{teach}\:{you}\:{a}\:{way}\:{to}\:{solve}\:{it}. \\ $$$$\mathrm{3}^{\mathrm{2}} +\mathrm{log}_{\mathrm{2}} \:\mathrm{2}=\mathrm{9}+\mathrm{1}=\mathrm{10}\:\Rightarrow{x}=\mathrm{2} \\ $$$${but}\:{if}\:{the}\:{equation}\:{is} \\ $$$$\mathrm{3}^{{x}} =\mathrm{20}−\mathrm{log}_{\mathrm{2}} \:{x} \\ $$$${you}\:{can}'{t}\:{solve}\:{it}\:{in}\:{the}\:{same}\:{way}. \\ $$
Commented by daus last updated on 17/May/22

$${ouh}\:{thanks}\: \\ $$
