Question Number 170148 by Shrinava last updated on 17/May/22
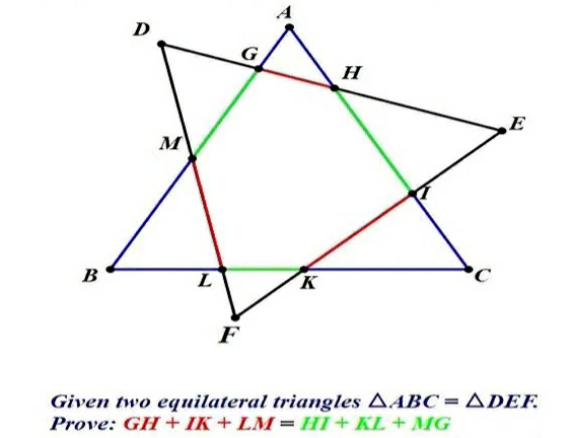
Answered by mr W last updated on 20/May/22
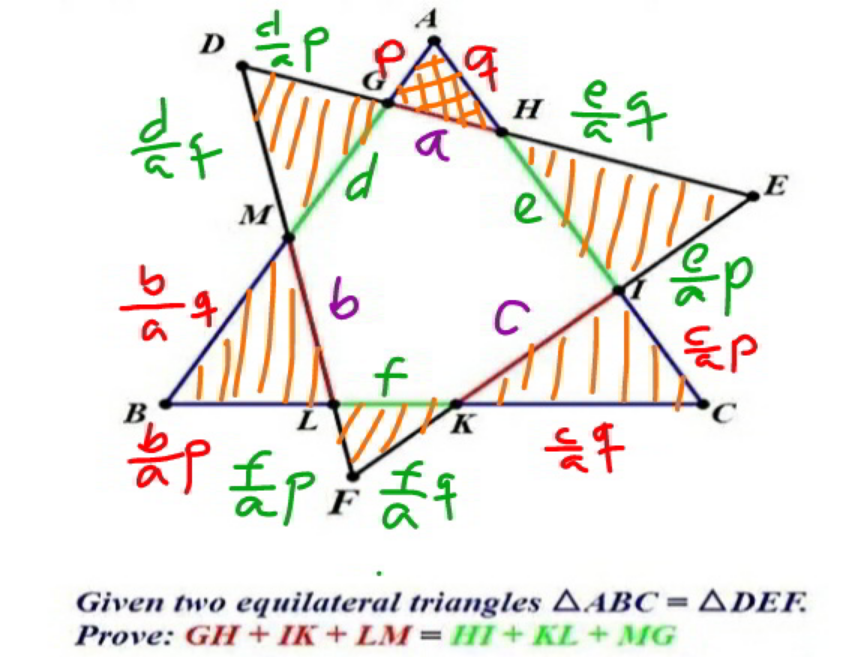
Commented by mr W last updated on 20/May/22
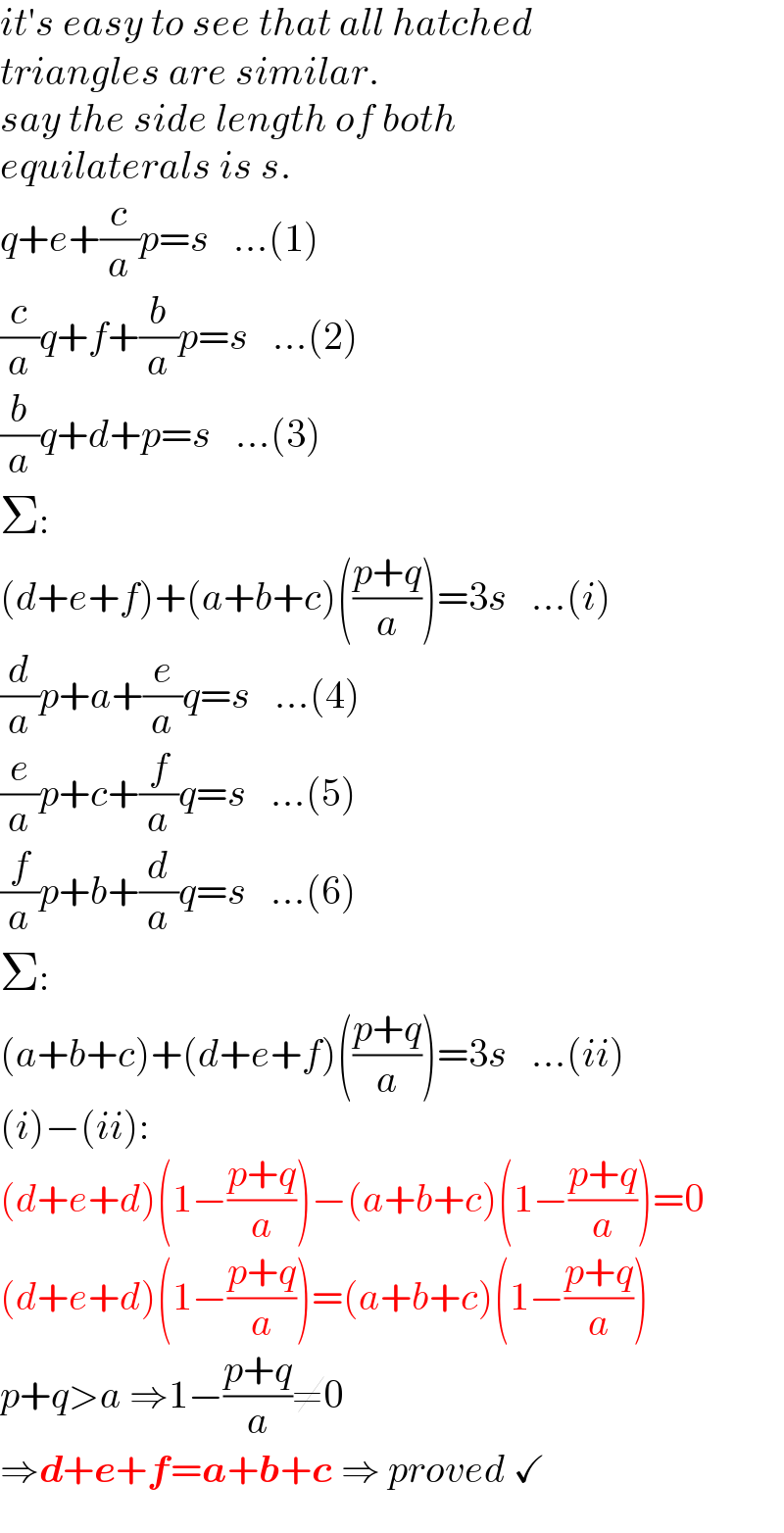
$${it}'{s}\:{easy}\:{to}\:{see}\:{that}\:{all}\:{hatched} \\ $$$${triangles}\:{are}\:{similar}. \\ $$$${say}\:{the}\:{side}\:{length}\:{of}\:{both}\: \\ $$$${equilaterals}\:{is}\:{s}. \\ $$$${q}+{e}+\frac{{c}}{{a}}{p}={s}\:\:\:…\left(\mathrm{1}\right) \\ $$$$\frac{{c}}{{a}}{q}+{f}+\frac{{b}}{{a}}{p}={s}\:\:\:…\left(\mathrm{2}\right) \\ $$$$\frac{{b}}{{a}}{q}+{d}+{p}={s}\:\:\:…\left(\mathrm{3}\right) \\ $$$$\Sigma: \\ $$$$\left({d}+{e}+{f}\right)+\left({a}+{b}+{c}\right)\left(\frac{{p}+{q}}{{a}}\right)=\mathrm{3}{s}\:\:\:…\left({i}\right) \\ $$$$\frac{{d}}{{a}}{p}+{a}+\frac{{e}}{{a}}{q}={s}\:\:\:…\left(\mathrm{4}\right) \\ $$$$\frac{{e}}{{a}}{p}+{c}+\frac{{f}}{{a}}{q}={s}\:\:\:…\left(\mathrm{5}\right) \\ $$$$\frac{{f}}{{a}}{p}+{b}+\frac{{d}}{{a}}{q}={s}\:\:\:…\left(\mathrm{6}\right) \\ $$$$\Sigma: \\ $$$$\left({a}+{b}+{c}\right)+\left({d}+{e}+{f}\right)\left(\frac{{p}+{q}}{{a}}\right)=\mathrm{3}{s}\:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\left({d}+{e}+{d}\right)\left(\mathrm{1}−\frac{{p}+{q}}{{a}}\right)−\left({a}+{b}+{c}\right)\left(\mathrm{1}−\frac{{p}+{q}}{{a}}\right)=\mathrm{0} \\ $$$$\left({d}+{e}+{d}\right)\left(\mathrm{1}−\frac{{p}+{q}}{{a}}\right)=\left({a}+{b}+{c}\right)\left(\mathrm{1}−\frac{{p}+{q}}{{a}}\right) \\ $$$${p}+{q}>{a}\:\Rightarrow\mathrm{1}−\frac{{p}+{q}}{{a}}\neq\mathrm{0} \\ $$$$\Rightarrow\boldsymbol{{d}}+\boldsymbol{{e}}+\boldsymbol{{f}}=\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}\:\Rightarrow\:{proved}\:\checkmark \\ $$
Commented by Shrinava last updated on 21/May/22
$$\mathrm{Fantastic}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{thank}\:\mathrm{yo}\:\mathrm{so}\:\mathrm{much} \\ $$
Commented by Tawa11 last updated on 08/Oct/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
