Question-170150

Question Number 170150 by daus last updated on 17/May/22

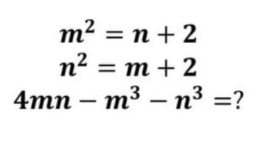
Answered by Rasheed.Sindhi last updated on 17/May/22

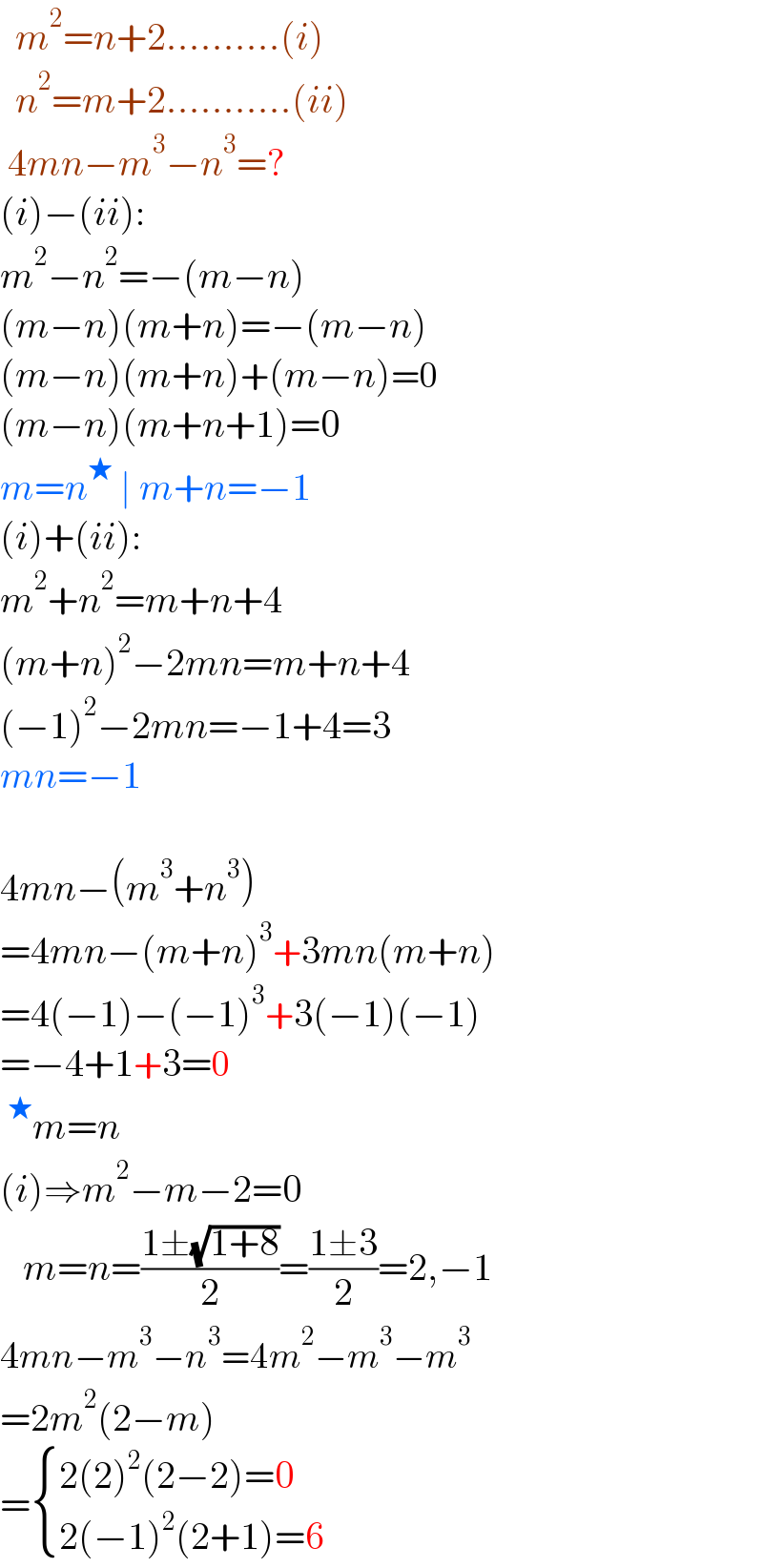
m^2 =n+2..........(i) n^2 =m+2...........(ii) 4mn−m^3 −n^3 =? (i)−(ii): m^2 −n^2 =−(m−n) (m−n)(m+n)=−(m−n) (m−n)(m+n)+(m−n)=0 (m−n)(m+n+1)=0 m=n^★ ∣ m+n=−1 (i)+(ii): m^2 +n^2 =m+n+4 (m+n)^2 −2mn=m+n+4 (−1)^2 −2mn=−1+4=3 mn=−1 4mn−(m^3 +n^3 ) =4mn−(m+n)^3 +3mn(m+n) =4(−1)−(−1)^3 +3(−1)(−1) =−4+1+3=0 ^★ m=n (i)⇒m^2 −m−2=0 m=n=((1±(√(1+8)))/2)=((1±3)/2)=2,−1 4mn−m^3 −n^3 =4m^2 −m^3 −m^3 =2m^2 (2−m) = { ((2(2)^2 (2−2)=0)),((2(−1)^2 (2+1)=6)) :}

$$\:\:{m}^{\mathrm{2}} ={n}+\mathrm{2}……….\left({i}\right) \\ $$$$\:\:{n}^{\mathrm{2}} ={m}+\mathrm{2}………..\left({ii}\right) \\ $$$$\:\mathrm{4}{mn}−{m}^{\mathrm{3}} −{n}^{\mathrm{3}} =? \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$${m}^{\mathrm{2}} −{n}^{\mathrm{2}} =−\left({m}−{n}\right) \\ $$$$\left({m}−{n}\right)\left({m}+{n}\right)=−\left({m}−{n}\right) \\ $$$$\left({m}−{n}\right)\left({m}+{n}\right)+\left({m}−{n}\right)=\mathrm{0} \\ $$$$\left({m}−{n}\right)\left({m}+{n}+\mathrm{1}\right)=\mathrm{0} \\ $$$${m}={n}^{\bigstar} \:\mid\:{m}+{n}=−\mathrm{1} \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$${m}^{\mathrm{2}} +{n}^{\mathrm{2}} ={m}+{n}+\mathrm{4} \\ $$$$\left({m}+{n}\right)^{\mathrm{2}} −\mathrm{2}{mn}={m}+{n}+\mathrm{4} \\ $$$$\left(−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}{mn}=−\mathrm{1}+\mathrm{4}=\mathrm{3} \\ $$$${mn}=−\mathrm{1} \\ $$$$ \\ $$$$\mathrm{4}{mn}−\left({m}^{\mathrm{3}} +{n}^{\mathrm{3}} \right) \\ $$$$=\mathrm{4}{mn}−\left({m}+{n}\right)^{\mathrm{3}} +\mathrm{3}{mn}\left({m}+{n}\right) \\ $$$$=\mathrm{4}\left(−\mathrm{1}\right)−\left(−\mathrm{1}\right)^{\mathrm{3}} +\mathrm{3}\left(−\mathrm{1}\right)\left(−\mathrm{1}\right) \\ $$$$=−\mathrm{4}+\mathrm{1}+\mathrm{3}=\mathrm{0} \\ $$$$\:^{\bigstar} {m}={n} \\ $$$$\left({i}\right)\Rightarrow{m}^{\mathrm{2}} −{m}−\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:{m}={n}=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{8}}}{\mathrm{2}}=\frac{\mathrm{1}\pm\mathrm{3}}{\mathrm{2}}=\mathrm{2},−\mathrm{1} \\ $$$$\mathrm{4}{mn}−{m}^{\mathrm{3}} −{n}^{\mathrm{3}} =\mathrm{4}{m}^{\mathrm{2}} −{m}^{\mathrm{3}} −{m}^{\mathrm{3}} \\ $$$$=\mathrm{2}{m}^{\mathrm{2}} \left(\mathrm{2}−{m}\right) \\ $$$$=\begin{cases}{\mathrm{2}\left(\mathrm{2}\right)^{\mathrm{2}} \left(\mathrm{2}−\mathrm{2}\right)=\mathrm{0}}\\{\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}+\mathrm{1}\right)=\mathrm{6}}\end{cases} \\ $$

Commented by peter frank last updated on 19/May/22

$$\mathrm{thanks} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply