Question Number 170187 by infinityaction last updated on 18/May/22
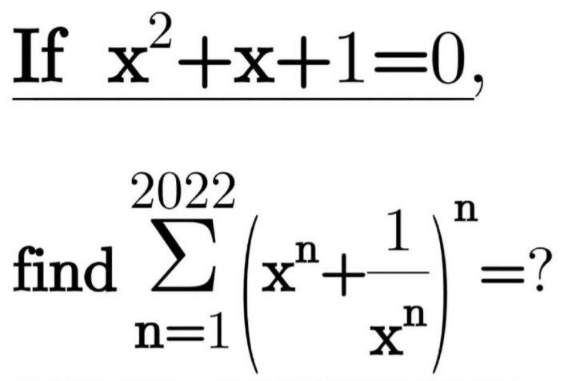
Commented by MJS_new last updated on 18/May/22
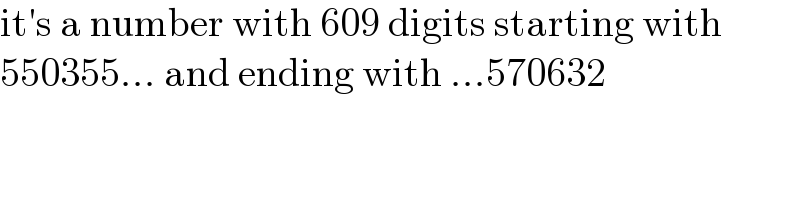
$$\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{number}\:\mathrm{with}\:\mathrm{609}\:\mathrm{digits}\:\mathrm{starting}\:\mathrm{with} \\ $$$$\mathrm{550355}…\:\mathrm{and}\:\mathrm{ending}\:\mathrm{with}\:…\mathrm{570632} \\ $$
Commented by infinityaction last updated on 19/May/22
X+1/x=-1
X²+1/x²=-1
X³+1/x³=2
X²+x+1=0
Multiply both side by x-1
We will get
X³-1=0
X³=1
X⁴=x
X⁵=x²
X⁶=x³=1
So we can say
X^(3k+1)=x
X^(3k+2)=x²
X^3k=1
So
X^(3k+1) + 1/x^(3k+1) and x^(3k+2) + 1/x^(3k+2) will get cancel because
X^(3k+1) + 1/x^(3k+1) will get even power
So -1^(any even term)=1
And
X^(3k+2) +1/x^(3k+2) will get odd power because 3k+2= odd term
So
(-1)^( any odd number)=-1
1+(-1)=0
So now basically we just have to find the sum of (x^3k+1/x^3k)^3k
So
That will be equal to
2^3k ( for k=1,2,3..... 674)
So now will use the formula of sum of gp
So sum will be 8(8⁶⁷⁴-1)/7
Commented by infinityaction last updated on 19/May/22
$${sir}\:{please}\:{check}\:{my}\:{solution} \\ $$
Answered by Rasheed.Sindhi last updated on 18/May/22
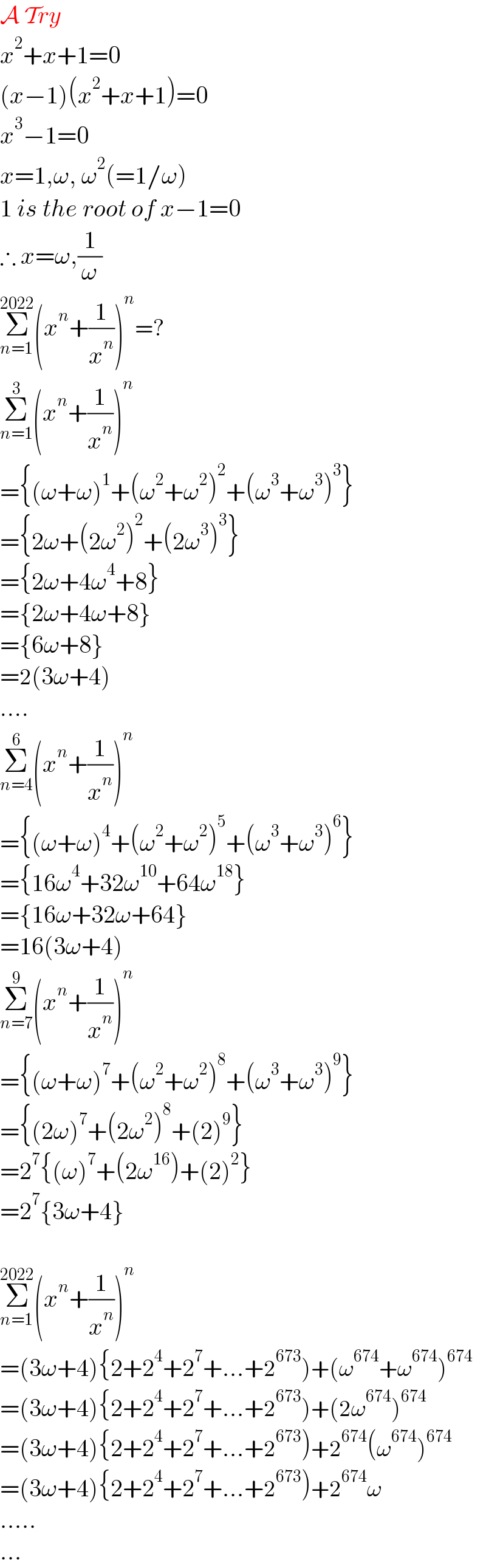
$$\mathcal{A}\:\mathcal{T}{ry} \\ $$$${x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{3}} −\mathrm{1}=\mathrm{0} \\ $$$${x}=\mathrm{1},\omega,\:\omega^{\mathrm{2}} \left(=\mathrm{1}/\omega\right) \\ $$$$\mathrm{1}\:{is}\:{the}\:{root}\:{of}\:{x}−\mathrm{1}=\mathrm{0} \\ $$$$\therefore\:{x}=\omega,\frac{\mathrm{1}}{\omega} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{2022}} {\sum}}\left({x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }\right)^{{n}} =? \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{3}} {\sum}}\left({x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }\right)^{{n}} \\ $$$$=\left\{\left(\omega+\omega\right)^{\mathrm{1}} +\left(\omega^{\mathrm{2}} +\omega^{\mathrm{2}} \right)^{\mathrm{2}} +\left(\omega^{\mathrm{3}} +\omega^{\mathrm{3}} \right)^{\mathrm{3}} \right\} \\ $$$$=\left\{\mathrm{2}\omega+\left(\mathrm{2}\omega^{\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{2}\omega^{\mathrm{3}} \right)^{\mathrm{3}} \right\} \\ $$$$=\left\{\mathrm{2}\omega+\mathrm{4}\omega^{\mathrm{4}} +\mathrm{8}\right\} \\ $$$$=\left\{\mathrm{2}\omega+\mathrm{4}\omega+\mathrm{8}\right\} \\ $$$$=\left\{\mathrm{6}\omega+\mathrm{8}\right\} \\ $$$$=\mathrm{2}\left(\mathrm{3}\omega+\mathrm{4}\right) \\ $$$$…. \\ $$$$\underset{{n}=\mathrm{4}} {\overset{\mathrm{6}} {\sum}}\left({x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }\right)^{{n}} \\ $$$$=\left\{\left(\omega+\omega\right)^{\mathrm{4}} +\left(\omega^{\mathrm{2}} +\omega^{\mathrm{2}} \right)^{\mathrm{5}} +\left(\omega^{\mathrm{3}} +\omega^{\mathrm{3}} \right)^{\mathrm{6}} \right\} \\ $$$$=\left\{\mathrm{16}\omega^{\mathrm{4}} +\mathrm{32}\omega^{\mathrm{10}} +\mathrm{64}\omega^{\mathrm{18}} \right\} \\ $$$$=\left\{\mathrm{16}\omega+\mathrm{32}\omega+\mathrm{64}\right\} \\ $$$$=\mathrm{16}\left(\mathrm{3}\omega+\mathrm{4}\right) \\ $$$$\underset{{n}=\mathrm{7}} {\overset{\mathrm{9}} {\sum}}\left({x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }\right)^{{n}} \\ $$$$=\left\{\left(\omega+\omega\right)^{\mathrm{7}} +\left(\omega^{\mathrm{2}} +\omega^{\mathrm{2}} \right)^{\mathrm{8}} +\left(\omega^{\mathrm{3}} +\omega^{\mathrm{3}} \right)^{\mathrm{9}} \right\} \\ $$$$=\left\{\left(\mathrm{2}\omega\right)^{\mathrm{7}} +\left(\mathrm{2}\omega^{\mathrm{2}} \right)^{\mathrm{8}} +\left(\mathrm{2}\right)^{\mathrm{9}} \right\} \\ $$$$=\mathrm{2}^{\mathrm{7}} \left\{\left(\omega\right)^{\mathrm{7}} +\left(\mathrm{2}\omega^{\mathrm{16}} \right)+\left(\mathrm{2}\right)^{\mathrm{2}} \right\} \\ $$$$=\mathrm{2}^{\mathrm{7}} \left\{\mathrm{3}\omega+\mathrm{4}\right\} \\ $$$$ \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\mathrm{2022}} {\sum}}\left({x}^{{n}} +\frac{\mathrm{1}}{{x}^{{n}} }\right)^{{n}} \\ $$$$=\left(\mathrm{3}\omega+\mathrm{4}\right)\left\{\mathrm{2}+\mathrm{2}^{\mathrm{4}} +\mathrm{2}^{\mathrm{7}} +…+\mathrm{2}^{\mathrm{673}} \right)+\left(\omega^{\mathrm{674}} +\omega^{\mathrm{674}} \right)^{\mathrm{674}} \\ $$$$=\left(\mathrm{3}\omega+\mathrm{4}\right)\left\{\mathrm{2}+\mathrm{2}^{\mathrm{4}} +\mathrm{2}^{\mathrm{7}} +…+\mathrm{2}^{\mathrm{673}} \right)+\left(\mathrm{2}\omega^{\mathrm{674}} \right)^{\mathrm{674}} \\ $$$$=\left(\mathrm{3}\omega+\mathrm{4}\right)\left\{\mathrm{2}+\mathrm{2}^{\mathrm{4}} +\mathrm{2}^{\mathrm{7}} +…+\mathrm{2}^{\mathrm{673}} \right)+\mathrm{2}^{\mathrm{674}} \left(\omega^{\mathrm{674}} \right)^{\mathrm{674}} \\ $$$$=\left(\mathrm{3}\omega+\mathrm{4}\right)\left\{\mathrm{2}+\mathrm{2}^{\mathrm{4}} +\mathrm{2}^{\mathrm{7}} +…+\mathrm{2}^{\mathrm{673}} \right)+\mathrm{2}^{\mathrm{674}} \omega \\ $$$$….. \\ $$$$… \\ $$
