Question Number 170197 by mathlove last updated on 18/May/22
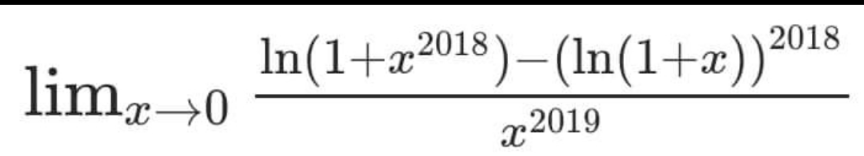
Answered by qaz last updated on 18/May/22
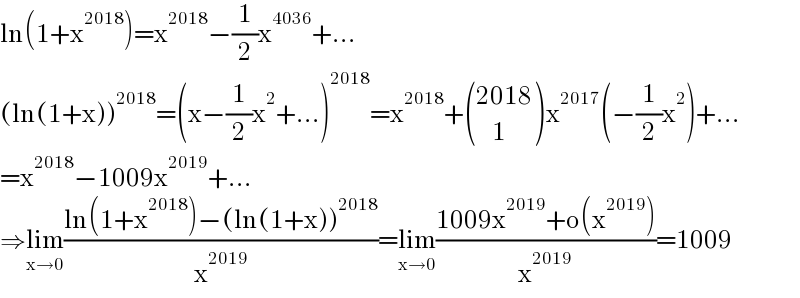
$$\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2018}} \right)=\mathrm{x}^{\mathrm{2018}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{4036}} +… \\ $$$$\left(\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\right)^{\mathrm{2018}} =\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +…\right)^{\mathrm{2018}} =\mathrm{x}^{\mathrm{2018}} +\begin{pmatrix}{\mathrm{2018}}\\{\:\:\:\:\mathrm{1}}\end{pmatrix}\mathrm{x}^{\mathrm{2017}} \left(−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \right)+… \\ $$$$=\mathrm{x}^{\mathrm{2018}} −\mathrm{1009x}^{\mathrm{2019}} +… \\ $$$$\Rightarrow\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2018}} \right)−\left(\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\right)^{\mathrm{2018}} }{\mathrm{x}^{\mathrm{2019}} }=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1009x}^{\mathrm{2019}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{2019}} \right)}{\mathrm{x}^{\mathrm{2019}} }=\mathrm{1009} \\ $$
