Question Number 170284 by sciencestudent last updated on 19/May/22
Commented by sciencestudent last updated on 19/May/22
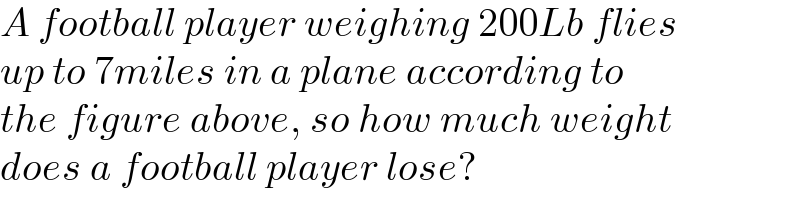
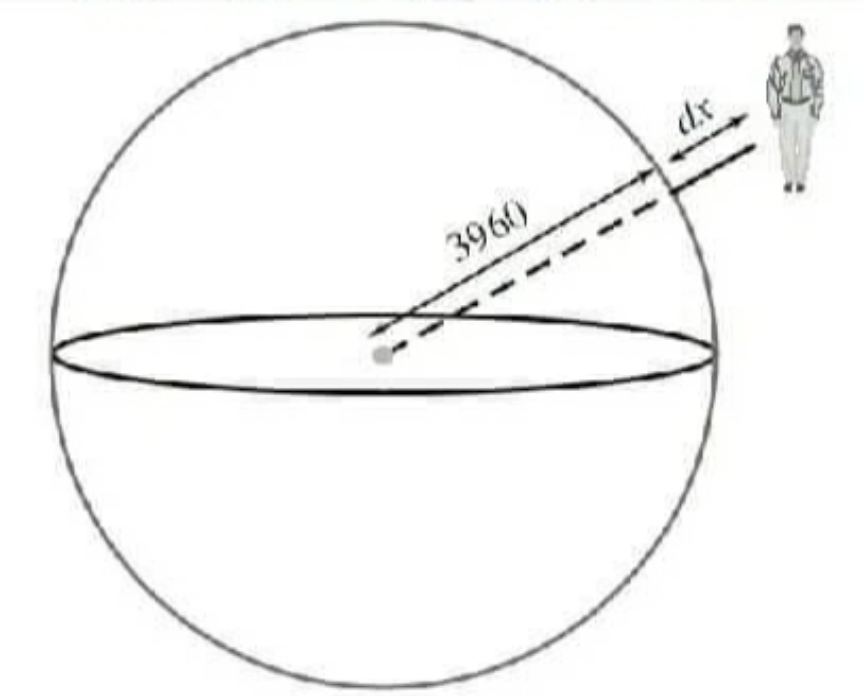
$${A}\:{football}\:{player}\:{weighing}\:\mathrm{200}{Lb}\:{flies} \\ $$$${up}\:{to}\:\mathrm{7}{miles}\:{in}\:{a}\:{plane}\:{according}\:{to} \\ $$$${the}\:{figure}\:{above},\:{so}\:{how}\:{much}\:{weight} \\ $$$${does}\:{a}\:{football}\:{player}\:{lose}? \\ $$
Commented by sciencestudent last updated on 19/May/22
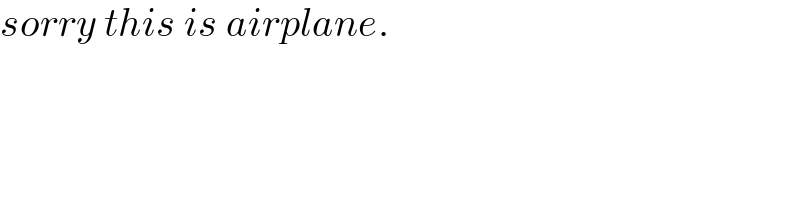
$${sorry}\:{this}\:{is}\:{airplane}. \\ $$
Commented by sciencestudent last updated on 19/May/22
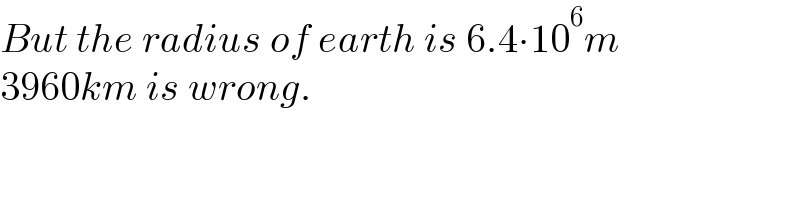
$${But}\:{the}\:{radius}\:{of}\:{earth}\:{is}\:\mathrm{6}.\mathrm{4}\centerdot\mathrm{10}^{\mathrm{6}} {m} \\ $$$$\mathrm{3960}{km}\:{is}\:{wrong}. \\ $$
Commented by mr W last updated on 20/May/22

$${R}=\mathrm{3960}\:{miles},\:{not}\:\mathrm{3960}\:{km}! \\ $$
Commented by mr W last updated on 20/May/22
![if the weight of a man on the surface of earth is W, and its weight at a height h is W_h , then W=((GMm)/R^2 ) W_h =((GMm)/((R+h)^2 )) we get: W_h =((R/(R+h)))^2 W < W the weight he loses at height h is ΔW=W−W_h =[1−((R/(R+h)))^2 ]W =[1−(((3960)/(3960+7)))^2 ]×200=0.705 lb](https://www.tinkutara.com/question/Q170302.png)
$${if}\:{the}\:{weight}\:{of}\:{a}\:{man}\:{on}\:{the}\:{surface}\: \\ $$$${of}\:{earth}\:{is}\:{W},\:{and}\:{its}\:{weight}\:{at}\:{a} \\ $$$${height}\:{h}\:{is}\:{W}_{{h}} ,\:{then} \\ $$$${W}=\frac{{GMm}}{{R}^{\mathrm{2}} } \\ $$$${W}_{{h}} =\frac{{GMm}}{\left({R}+{h}\right)^{\mathrm{2}} } \\ $$$${we}\:{get}: \\ $$$${W}_{{h}} =\left(\frac{{R}}{{R}+{h}}\right)^{\mathrm{2}} {W}\:<\:{W} \\ $$$${the}\:{weight}\:{he}\:{loses}\:{at}\:{height}\:{h}\:{is} \\ $$$$\Delta{W}={W}−{W}_{{h}} =\left[\mathrm{1}−\left(\frac{{R}}{{R}+{h}}\right)^{\mathrm{2}} \right]{W} \\ $$$$=\left[\mathrm{1}−\left(\frac{\mathrm{3960}}{\mathrm{3960}+\mathrm{7}}\right)^{\mathrm{2}} \right]×\mathrm{200}=\mathrm{0}.\mathrm{705}\:{lb} \\ $$
Commented by Tawa11 last updated on 08/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
