Question Number 170290 by muneer0o0 last updated on 19/May/22

Commented by Engr_Jidda last updated on 19/May/22
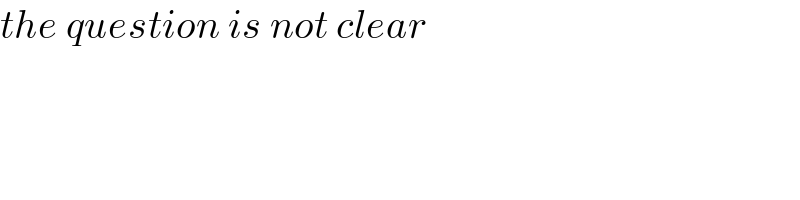
$${the}\:{question}\:{is}\:{not}\:{clear} \\ $$
Answered by Mathspace last updated on 21/May/22
![i f the Q is ∫_0 ^2 ∫_x ^(√(4−x^2 )) ((x/y))^2 dy dx ⇒I=∫_0 ^2 (∫_x ^(√(4−x^2 )) (1/y^2 )dy)x^2 dx =∫_0 ^2 ([−(1/y)]_x ^(√(4−x^2 )) )x^2 dx =∫_0 ^2 x^2 ((1/x)−(1/( (√(4−x^2 )))))dx =∫_0 ^2 xdx−∫_0 ^2 (x^2 /( (√(4−x^2 ))))dx =[(x^2 /2)]_0 ^2 −∫_0 ^2 (x^2 /( (√(4−x^2 ))))dx =2+∫_0 ^2 ((4−x^2 −4)/( (√(4−x^2 ))))dx =2+∫_0 ^2 (√(4−x^2 ))dx+4∫_0 ^2 (dx/( (√(4−x^2 )))) we have ∫_0 ^2 (√(4−x^2 ))dx=_(x=2sinθ) ∫_0 ^(π/2) 2cosθ(2cosθ)dθ =4∫_0 ^(π/2) cos^2 (θ)dθ=2∫_0 ^(π/2) (1+cos(2θ))dθ =π +[sin(2θ)]_0 ^(π/2) =π ∫_0 ^2 (dx/( (√(4−x^2 ))))=_(x=2t) ∫_0 ^1 ((2dt)/(2(√(1−t^2 )))) =[arcsint]_0 ^1 =(π/2) ⇒ I=2+π+2π =2+3π](https://www.tinkutara.com/question/Q170348.png)
$${i}\:{f}\:{the}\:{Q}\:{is}\:\int_{\mathrm{0}} ^{\mathrm{2}} \int_{{x}} ^{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }} \left(\frac{{x}}{{y}}\right)^{\mathrm{2}} {dy}\:{dx} \\ $$$$\Rightarrow{I}=\int_{\mathrm{0}} ^{\mathrm{2}} \left(\int_{{x}} ^{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }} \frac{\mathrm{1}}{{y}^{\mathrm{2}} }{dy}\right){x}^{\mathrm{2}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} \left(\left[−\frac{\mathrm{1}}{{y}}\right]_{{x}} ^{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }} \right){x}^{\mathrm{2}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} {x}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} {xdx}−\int_{\mathrm{0}} ^{\mathrm{2}} \frac{{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}{dx} \\ $$$$=\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{2}} −\int_{\mathrm{0}} ^{\mathrm{2}} \frac{{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}{dx} \\ $$$$=\mathrm{2}+\int_{\mathrm{0}} ^{\mathrm{2}} \frac{\mathrm{4}−{x}^{\mathrm{2}} −\mathrm{4}}{\:\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}{dx} \\ $$$$=\mathrm{2}+\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\mathrm{4}−{x}^{\mathrm{2}} }{dx}+\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{2}} \frac{{dx}}{\:\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }} \\ $$$${we}\:{have} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\mathrm{4}−{x}^{\mathrm{2}} }{dx}=_{{x}=\mathrm{2}{sin}\theta} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{2}{cos}\theta\left(\mathrm{2}{cos}\theta\right){d}\theta \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}} \left(\theta\right){d}\theta=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)\right){d}\theta \\ $$$$=\pi\:+\left[{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\pi \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \frac{{dx}}{\:\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }}=_{{x}=\mathrm{2}{t}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{dt}}{\mathrm{2}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }} \\ $$$$=\left[{arcsint}\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$${I}=\mathrm{2}+\pi+\mathrm{2}\pi\:=\mathrm{2}+\mathrm{3}\pi \\ $$
Commented by Tawa11 last updated on 08/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
