Question Number 17053 by I’m a gamer last updated on 30/Jun/17
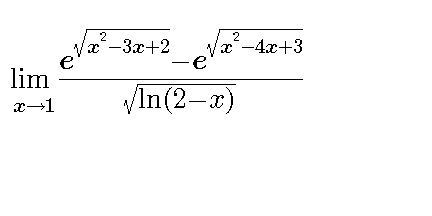
Answered by ajfour last updated on 30/Jun/17
![L=lim_(x→1) ((e^(√A) −e^(√B) )/( (√(ln (1+(1−x))))) =lim_(x→1) (1/(e^(√A) +e^(√B) ))×(((e^A −e^B ))/( (√((1−x)−(((1−x)^2 )/2)+..)))) =(1/2)×lim_(x→1) (((1+A+(A^2 /2)+..)−(1+B+(B^2 /2)−..))/(∣1−x∣(√(1−(((1−x))/2)+..)))) =(1/2)×lim_(x→1) (((A−B)[1+((A+B)/2)+..])/(∣1−x∣(√(1−(((1−x))/2)+..)))) L=(1/2)×lim_(x→1) (((x−1))/(∣x−1∣))×lim_(x→1) (([1+((A+B)/2)+..])/( (√(1−(((1−x))/2)+..)))) L=(1/2)×lim_(x→1) ((x−1)/(∣x−1∣)) . R.H.L.=(1/2) ; L.H.L.=−(1/2) limit dont exist at x=1.](https://www.tinkutara.com/question/Q17066.png)
$$\mathrm{L}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{e}^{\sqrt{\mathrm{A}}} −\mathrm{e}^{\sqrt{\mathrm{B}}} }{\:\sqrt{\mathrm{ln}\:\left(\mathrm{1}+\left(\mathrm{1}−\mathrm{x}\right)\right.}} \\ $$$$\:\:=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{e}^{\sqrt{\mathrm{A}}} +\mathrm{e}^{\sqrt{\mathrm{B}}} }×\frac{\left(\mathrm{e}^{\mathrm{A}} −\mathrm{e}^{\mathrm{B}} \right)}{\:\sqrt{\left(\mathrm{1}−\mathrm{x}\right)−\frac{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }{\mathrm{2}}+..}}\: \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}×\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\left(\mathrm{1}+\mathrm{A}+\frac{\mathrm{A}^{\mathrm{2}} }{\mathrm{2}}+..\right)−\left(\mathrm{1}+\mathrm{B}+\frac{\mathrm{B}^{\mathrm{2}} }{\mathrm{2}}−..\right)}{\mid\mathrm{1}−\mathrm{x}\mid\sqrt{\mathrm{1}−\frac{\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{2}}+..}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left(\mathrm{A}−\mathrm{B}\right)\left[\mathrm{1}+\frac{\mathrm{A}+\mathrm{B}}{\mathrm{2}}+..\right]}{\mid\mathrm{1}−\mathrm{x}\mid\sqrt{\mathrm{1}−\frac{\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{2}}+..}}\: \\ $$$$\mathrm{L}=\frac{\mathrm{1}}{\mathrm{2}}×\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left(\mathrm{x}−\mathrm{1}\right)}{\mid\mathrm{x}−\mathrm{1}\mid}×\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left[\mathrm{1}+\frac{\mathrm{A}+\mathrm{B}}{\mathrm{2}}+..\right]}{\:\sqrt{\mathrm{1}−\frac{\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{2}}+..}}\: \\ $$$$\boldsymbol{\mathrm{L}}=\frac{\mathrm{1}}{\mathrm{2}}×\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{x}−\mathrm{1}}{\mid\mathrm{x}−\mathrm{1}\mid}\:. \\ $$$$\mathrm{R}.\mathrm{H}.\mathrm{L}.=\frac{\mathrm{1}}{\mathrm{2}}\:;\:\:\mathrm{L}.\mathrm{H}.\mathrm{L}.=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{limit}\:\mathrm{dont}\:\mathrm{exist}\:\mathrm{at}\:\mathrm{x}=\mathrm{1}. \\ $$
