Question Number 170552 by ajfour last updated on 26/May/22
Commented by ajfour last updated on 26/May/22

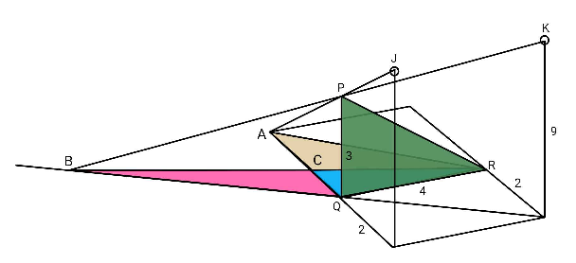
$${J}\:{and}\:{K}\:{are}\:{pole}\:{lights}.\:{The} \\ $$$${green}\:{triangle}\:{is}\:{vertical}. \\ $$$${Find}\:{area}\:{of}\:\bigtriangleup{ACR}. \\ $$
Answered by mr W last updated on 26/May/22

Commented by mr W last updated on 26/May/22

$$\frac{{AJ}'}{{AQ}}=\frac{\mathrm{9}}{\mathrm{3}}=\mathrm{3} \\ $$$$\frac{{AQ}+\mathrm{2}}{{AQ}}=\mathrm{3}\:\Rightarrow{AQ}=\mathrm{1} \\ $$$$\frac{{CQ}}{{RK}'}=\frac{{BQ}}{{BK}'}=\frac{\mathrm{3}}{\mathrm{9}}=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow{CQ}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${AC}=\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Delta_{{ACR}} =\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{3}}×\mathrm{4}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by ajfour last updated on 27/May/22

$${most}\:{lucid}\:{n}\:{elegant}\:{way}! \\ $$$${thank}\:{you}\:{sir}. \\ $$
Commented by Tawa11 last updated on 08/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
