Question Number 170568 by mathlove last updated on 27/May/22

Answered by Rasheed.Sindhi last updated on 27/May/22

$$\begin{array}{|c|}{\underset{\:\mathrm{f}\left(\mathrm{x}−\mathrm{1}\right)+\mathrm{g}\left(\mathrm{2x}+\mathrm{1}\right)=\mathrm{2x}\:\:\:\:\:\:\:\:\:\:} {\mathrm{f}\left(\mathrm{2x}+\mathrm{2}\right)+\mathrm{2g}\left(\mathrm{4x}+\mathrm{7}\right)=\mathrm{x}−\mathrm{1}}}\\\hline\end{array} \\ $$$$\left(\mathrm{1}\right):\:\:\:\:\mathrm{2x}+\mathrm{2}=\mathrm{y}\Rightarrow\mathrm{x}=\frac{\mathrm{y}−\mathrm{2}}{\mathrm{2}}\:: \\ $$$$\:\:\:\:\mathrm{f}\left(\mathrm{y}\right)+\mathrm{2g}\left(\mathrm{4}\centerdot\frac{\mathrm{y}−\mathrm{2}}{\mathrm{2}}+\mathrm{7}\right)=\frac{\mathrm{y}−\mathrm{2}}{\mathrm{2}}−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\Rightarrow\mathrm{f}\left(\mathrm{y}\right)+\mathrm{2g}\left(\mathrm{2y}+\mathrm{3}\right)=\frac{\mathrm{y}−\mathrm{4}}{\mathrm{2}}…\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{2}\right):\:\:\:\:\mathrm{x}−\mathrm{1}=\mathrm{y}\Rightarrow\mathrm{x}=\mathrm{y}+\mathrm{1} \\ $$$$\:\:\:\:\mathrm{f}\left(\mathrm{y}\right)+\mathrm{g}\left(\mathrm{2y}+\mathrm{3}\right)=\mathrm{2}\left(\mathrm{y}+\mathrm{1}\right)…\left(\mathrm{4}\right) \\ $$$$\left(\mathrm{3}\right)−\left(\mathrm{4}\right):\:\mathrm{g}\left(\mathrm{2y}+\mathrm{3}\right)=\frac{\mathrm{y}−\mathrm{4}}{\mathrm{2}}−\mathrm{2y}−\mathrm{2}=\frac{\mathrm{y}−\mathrm{4}−\mathrm{4y}−\mathrm{4}}{\mathrm{2}} \\ $$$$\mathrm{g}\left(\mathrm{2y}+\mathrm{3}\right)=\frac{−\mathrm{3y}−\mathrm{8}}{\mathrm{2}} \\ $$$$\mathrm{2y}+\mathrm{3}=\mathrm{x}\Rightarrow\mathrm{y}=\frac{\mathrm{x}−\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\frac{−\mathrm{3}\left(\frac{\mathrm{x}−\mathrm{3}}{\mathrm{2}}\right)−\mathrm{8}}{\mathrm{2}}=\frac{−\mathrm{3x}+\mathrm{9}−\mathrm{16}}{\mathrm{4}} \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\frac{−\mathrm{3x}−\mathrm{7}}{\mathrm{4}} \\ $$$$\left(\mathrm{3}\right):\:\mathrm{f}\left(\mathrm{y}\right)+\mathrm{2g}\left(\mathrm{2y}+\mathrm{3}\right)=\frac{\mathrm{y}−\mathrm{4}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)+\mathrm{2g}\left(\mathrm{2x}+\mathrm{3}\right)=\frac{\mathrm{x}−\mathrm{4}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}−\mathrm{4}}{\mathrm{2}}−\mathrm{2g}\left(\mathrm{2x}+\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}−\mathrm{4}}{\mathrm{2}}−\mathrm{2}\left(\frac{−\mathrm{3}\left(\mathrm{2x}+\mathrm{3}\right)−\mathrm{7}}{\mathrm{4}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{x}−\mathrm{4}}{\mathrm{2}}−\frac{−\mathrm{6x}−\mathrm{9}−\mathrm{7}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{x}−\mathrm{4}}{\mathrm{2}}+\frac{\mathrm{6x}+\mathrm{16}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{7x}+\mathrm{12}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{7x}+\mathrm{12}}{\mathrm{2}}\:,\:\mathrm{g}\left(\mathrm{x}\right)=\frac{−\mathrm{3x}−\mathrm{7}}{\mathrm{4}} \\ $$$$\mathrm{Pl}\:\mathrm{confirm}\:\mathrm{the}\:\mathrm{answers} \\ $$
Commented by Rasheed.Sindhi last updated on 27/May/22

$$\mathcal{VERIFICATION}: \\ $$$$\begin{array}{|c|}{\underset{\:\mathrm{f}\left(\mathrm{x}−\mathrm{1}\right)+\mathrm{g}\left(\mathrm{2x}+\mathrm{1}\right)=\mathrm{2x}\:\:\:\:\:\:\:\:\:\:} {\mathrm{f}\left(\mathrm{2x}+\mathrm{2}\right)+\mathrm{2g}\left(\mathrm{4x}+\mathrm{7}\right)=\mathrm{x}−\mathrm{1}}}\\\hline\end{array}\: \\ $$$$\bullet\mathrm{f}\left(\mathrm{2x}+\mathrm{2}\right)+\mathrm{2g}\left(\mathrm{4x}+\mathrm{7}\right)=\mathrm{x}−\mathrm{1} \\ $$$$\frac{\mathrm{7}\left(\mathrm{2x}+\mathrm{2}\right)+\mathrm{12}}{\mathrm{2}}+\mathrm{2}\left(\frac{−\mathrm{3}\left(\mathrm{4x}+\mathrm{7}\right)−\mathrm{7}}{\mathrm{4}}\right)=\mathrm{x}−\mathrm{1} \\ $$$$\frac{\mathrm{14x}+\mathrm{14}+\mathrm{12}}{\mathrm{2}}+\mathrm{2}\left(\frac{−\mathrm{12x}−\mathrm{21}−\mathrm{7}}{\mathrm{4}}\right)=\mathrm{x}−\mathrm{1} \\ $$$$\frac{\mathrm{14x}+\mathrm{26}}{\mathrm{2}}+\frac{−\mathrm{12x}−\mathrm{28}}{\mathrm{2}}=\mathrm{x}−\mathrm{1} \\ $$$$\mathrm{7x}+\mathrm{13}−\mathrm{6x}−\mathrm{14}=\mathrm{x}−\mathrm{1} \\ $$$$\mathrm{x}−\mathrm{1}=\mathrm{x}−\mathrm{1}\checkmark \\ $$$$\:\bullet\mathrm{f}\left(\mathrm{x}−\mathrm{1}\right)+\mathrm{g}\left(\mathrm{2x}+\mathrm{1}\right)=\mathrm{2x} \\ $$$$\frac{\mathrm{7}\left(\mathrm{x}−\mathrm{1}\right)+\mathrm{12}}{\mathrm{2}}+\frac{−\mathrm{3}\left(\mathrm{2x}+\mathrm{1}\right)−\mathrm{7}}{\mathrm{4}}=\mathrm{2x} \\ $$$$\frac{\mathrm{7x}−\mathrm{7}+\mathrm{12}}{\mathrm{2}}+\frac{−\mathrm{6x}−\mathrm{3}−\mathrm{7}}{\mathrm{4}}=\mathrm{2x} \\ $$$$\frac{\mathrm{7x}+\mathrm{5}}{\mathrm{2}}+\frac{−\mathrm{6x}−\mathrm{10}}{\mathrm{4}}=\mathrm{2x} \\ $$$$\frac{\mathrm{7x}+\mathrm{5}}{\mathrm{2}}+\frac{−\mathrm{3x}−\mathrm{5}}{\mathrm{2}}=\mathrm{2x} \\ $$$$\frac{\mathrm{4x}}{\mathrm{2}}=\mathrm{2x} \\ $$$$\mathrm{2x}=\mathrm{2x}\checkmark \\ $$
Commented by SLVR last updated on 31/May/22

$${dear}\:{sir}\:\:\:{how}\:{y}\:{variable}\:{has} \\ $$$$\mathrm{2}\:{notation}\:{y}=\mathrm{2}{x}+\mathrm{2}{and} \\ $$$${y}={x}−\mathrm{1}\:{at}\:{one}\:{go}…{kindly} \\ $$$${explain} \\ $$
Commented by Rasheed.Sindhi last updated on 31/May/22

$$\boldsymbol{{sir}}\:\boldsymbol{{mr}}\:\boldsymbol{{W}}\:{can}\:{better}\:{explain}. \\ $$$$\bullet\mathrm{f}\left(\mathrm{2x}+\mathrm{2}\right)+\mathrm{2g}\left(\mathrm{4x}+\mathrm{7}\right)=\mathrm{x}−\mathrm{1} \\ $$$$\bullet\:\mathrm{f}\left(\mathrm{x}−\mathrm{1}\right)+\mathrm{g}\left(\mathrm{2x}+\mathrm{1}\right)=\mathrm{2x} \\ $$$$\mathcal{T}{he}\:{two}\:{equations}\:{can}\:{be}\:{considerd} \\ $$$${separately}\:{with}\:{respect}\:{to}\:\mathrm{x}.\:{Actually} \\ $$$$\mathrm{x}\:{in}\:{one}\:{equation}\:{is}\:{nothing}\:{to}\:{do} \\ $$$${with}\:\mathrm{x}\:{in}\:{other}\:{equation}.\left(\mathcal{T}{hey}'{re}\right. \\ $$$${simultaneous}\:{only}\:{with}\:{respect} \\ $$$$\left.{to}\:\mathrm{f}\:{and}\:\mathrm{g}\:{only}\right).{Albeit}\:{all}\:{x}\:{in}\:{one}\:{equation} \\ $$$${are}\:{related}\:\:{to}\:{each}\:{other} \\ $$$${and}\:{all}\:{x}\:{in}\:{other}\:{equation}\:{are}\:{related}\:{to}\: \\ $$$${to}\:{each}\:{other}. \\ $$
Commented by Rasheed.Sindhi last updated on 31/May/22

$$\mathrm{These}\:\mathrm{equatios}\:\mathrm{are}\:\boldsymbol{\mathrm{separate}}\:\&\: \\ $$$$\left.\boldsymbol{\mathrm{simultaneous}}\:\mathrm{simultaneously}!\::\right) \\ $$
Commented by SLVR last updated on 31/May/22
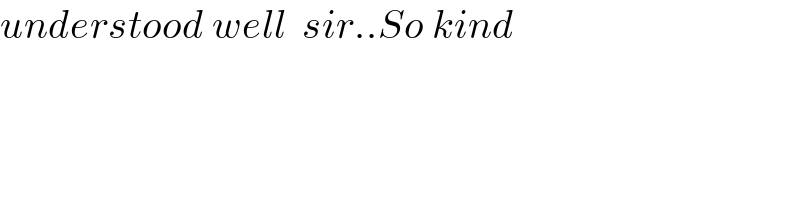
$${understood}\:{well}\:\:{sir}..{So}\:{kind} \\ $$
Commented by Rasheed.Sindhi last updated on 31/May/22

$${You}'{re}\:{welcome}\:{sir}! \\ $$
Commented by mathlove last updated on 02/Jun/22

$${thanks}\:{sir} \\ $$
Commented by mathlove last updated on 02/Jun/22

$${thank}\:{sir} \\ $$
Commented by Tawa11 last updated on 08/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
