Question Number 170572 by daus last updated on 27/May/22

Answered by mr W last updated on 27/May/22
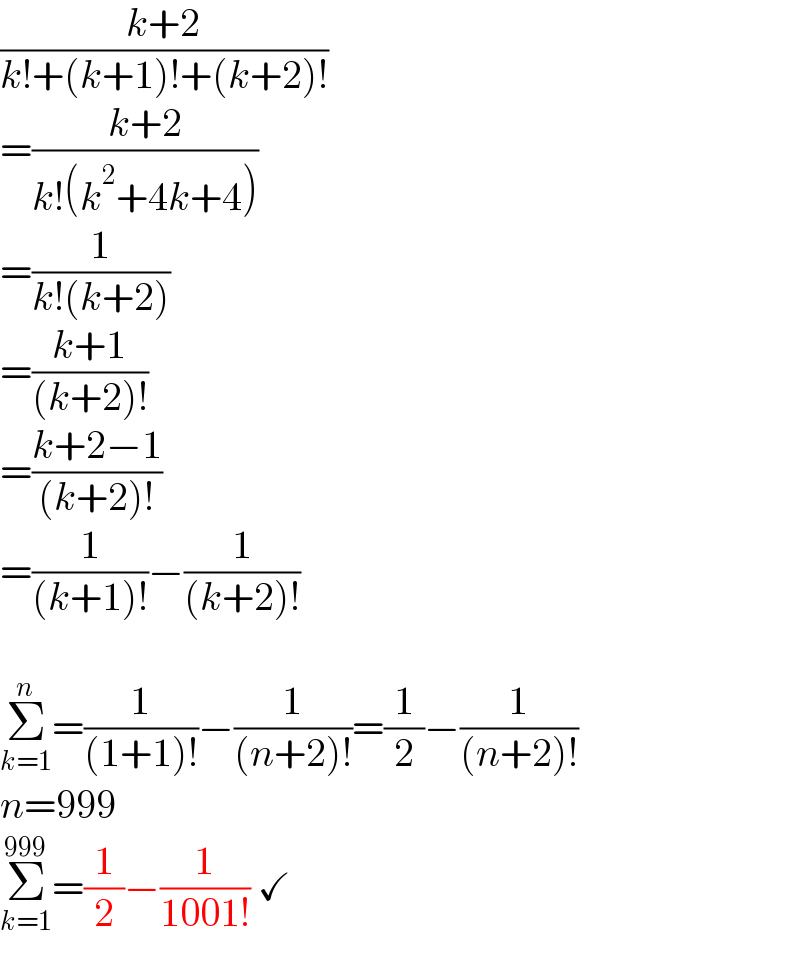
$$\frac{{k}+\mathrm{2}}{{k}!+\left({k}+\mathrm{1}\right)!+\left({k}+\mathrm{2}\right)!} \\ $$$$=\frac{{k}+\mathrm{2}}{{k}!\left({k}^{\mathrm{2}} +\mathrm{4}{k}+\mathrm{4}\right)} \\ $$$$=\frac{\mathrm{1}}{{k}!\left({k}+\mathrm{2}\right)} \\ $$$$=\frac{{k}+\mathrm{1}}{\left({k}+\mathrm{2}\right)!} \\ $$$$=\frac{{k}+\mathrm{2}−\mathrm{1}}{\left({k}+\mathrm{2}\right)!} \\ $$$$=\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)!}−\frac{\mathrm{1}}{\left({k}+\mathrm{2}\right)!} \\ $$$$ \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}=\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{1}\right)!}−\frac{\mathrm{1}}{\left({n}+\mathrm{2}\right)!}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\left({n}+\mathrm{2}\right)!} \\ $$$${n}=\mathrm{999} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\mathrm{999}} {\sum}}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{1001}!}\:\checkmark \\ $$
Commented by Tawa11 last updated on 08/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
