Question Number 170576 by Tawa11 last updated on 27/May/22

Commented by mr W last updated on 27/May/22
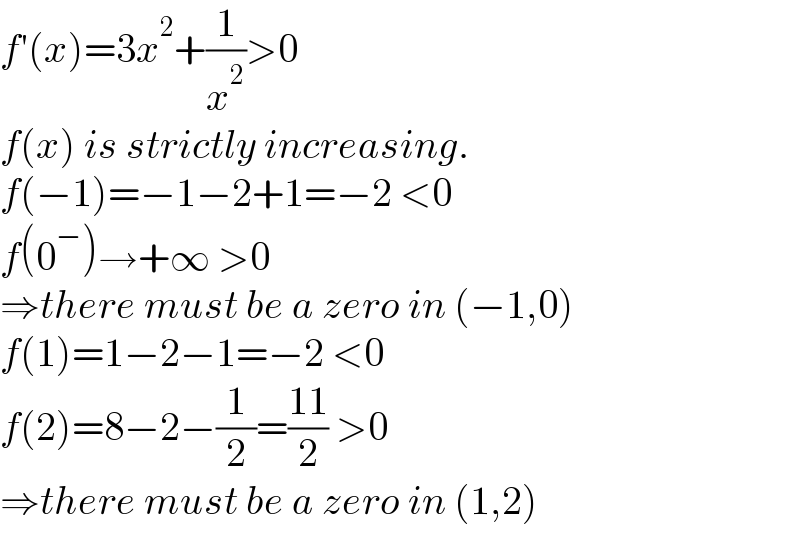
$${f}'\left({x}\right)=\mathrm{3}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }>\mathrm{0} \\ $$$${f}\left({x}\right)\:{is}\:{strictly}\:{increasing}. \\ $$$${f}\left(−\mathrm{1}\right)=−\mathrm{1}−\mathrm{2}+\mathrm{1}=−\mathrm{2}\:<\mathrm{0} \\ $$$${f}\left(\mathrm{0}^{−} \right)\rightarrow+\infty\:>\mathrm{0} \\ $$$$\Rightarrow{there}\:{must}\:{be}\:{a}\:{zero}\:{in}\:\left(−\mathrm{1},\mathrm{0}\right) \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1}−\mathrm{2}−\mathrm{1}=−\mathrm{2}\:<\mathrm{0} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{8}−\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{11}}{\mathrm{2}}\:>\mathrm{0} \\ $$$$\Rightarrow{there}\:{must}\:{be}\:{a}\:{zero}\:{in}\:\left(\mathrm{1},\mathrm{2}\right) \\ $$
Commented by Tawa11 last updated on 27/May/22
$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$
