Question Number 170593 by 119065 last updated on 27/May/22
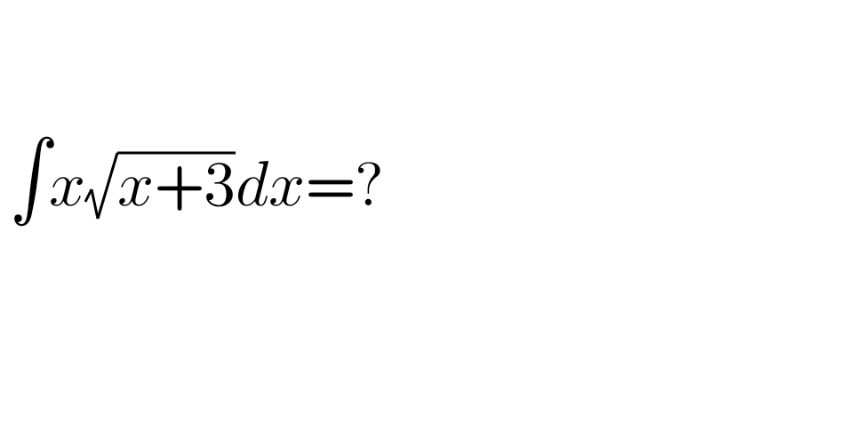
Commented by mkam last updated on 27/May/22
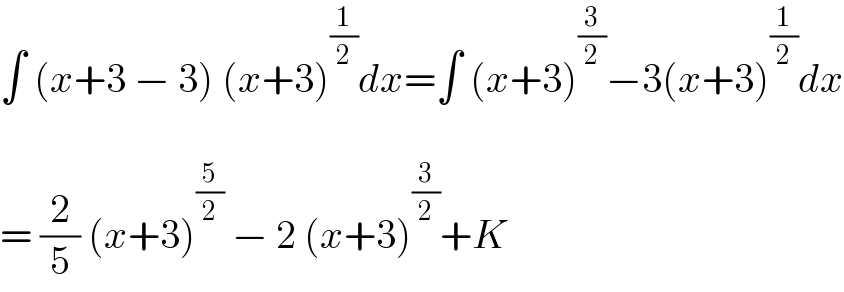
$$\int\:\left({x}+\mathrm{3}\:−\:\mathrm{3}\right)\:\left({x}+\mathrm{3}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dx}=\int\:\left({x}+\mathrm{3}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{3}\left({x}+\mathrm{3}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dx} \\ $$$$ \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{5}}\:\left({x}+\mathrm{3}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} \:−\:\mathrm{2}\:\left({x}+\mathrm{3}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +{K} \\ $$
Answered by greougoury555 last updated on 27/May/22
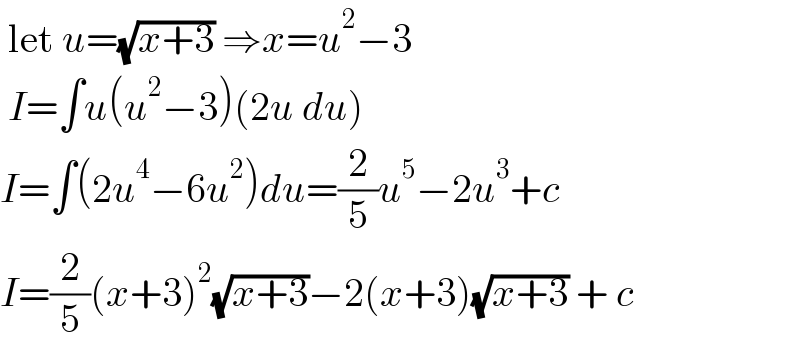
$$\:\mathrm{let}\:{u}=\sqrt{{x}+\mathrm{3}}\:\Rightarrow{x}={u}^{\mathrm{2}} −\mathrm{3} \\ $$$$\:{I}=\int{u}\left({u}^{\mathrm{2}} −\mathrm{3}\right)\left(\mathrm{2}{u}\:{du}\right) \\ $$$${I}=\int\left(\mathrm{2}{u}^{\mathrm{4}} −\mathrm{6}{u}^{\mathrm{2}} \right){du}=\frac{\mathrm{2}}{\mathrm{5}}{u}^{\mathrm{5}} −\mathrm{2}{u}^{\mathrm{3}} +{c} \\ $$$${I}=\frac{\mathrm{2}}{\mathrm{5}}\left({x}+\mathrm{3}\right)^{\mathrm{2}} \sqrt{{x}+\mathrm{3}}−\mathrm{2}\left({x}+\mathrm{3}\right)\sqrt{{x}+\mathrm{3}}\:+\:{c} \\ $$
Commented by 119065 last updated on 27/May/22
$${very}\:{good}\:{soulution} \\ $$
Answered by kndramaths last updated on 27/May/22
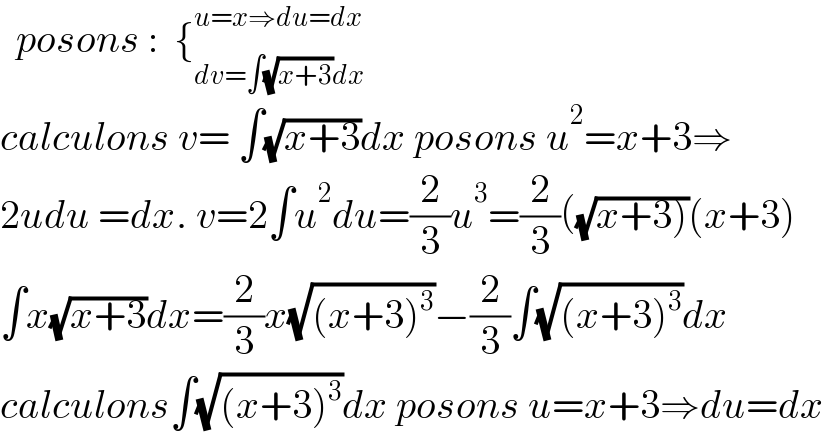
$$\:\:{posons}\::\:\:\left\{_{{dv}=\int\sqrt{{x}+\mathrm{3}}{dx}} ^{{u}={x}\Rightarrow{du}={dx}} \right. \\ $$$${calculons}\:{v}=\:\int\sqrt{{x}+\mathrm{3}}{dx}\:{posons}\:{u}^{\mathrm{2}} ={x}+\mathrm{3}\Rightarrow \\ $$$$\mathrm{2}{udu}\:={dx}.\:{v}=\mathrm{2}\int{u}^{\mathrm{2}} {du}=\frac{\mathrm{2}}{\mathrm{3}}{u}^{\mathrm{3}} =\frac{\mathrm{2}}{\mathrm{3}}\left(\sqrt{\left.{x}+\mathrm{3}\right)}\left({x}+\mathrm{3}\right)\right. \\ $$$$\int{x}\sqrt{{x}+\mathrm{3}}{dx}=\frac{\mathrm{2}}{\mathrm{3}}{x}\sqrt{\left({x}+\mathrm{3}\right)^{\mathrm{3}} }−\frac{\mathrm{2}}{\mathrm{3}}\int\sqrt{\left({x}+\mathrm{3}\right)^{\mathrm{3}} }{dx} \\ $$$${calculons}\int\sqrt{\left({x}+\mathrm{3}\right)^{\mathrm{3}} }{dx}\:{posons}\:{u}={x}+\mathrm{3}\Rightarrow{du}={dx} \\ $$
