Menu Close

Question-170601

Tinku Tara 0 Comments
Pin




Question Number 170601 by mr W last updated on 27/May/22
Commented by mr W last updated on 29/May/22
an uniform thin rope with length L is hanging at one end at a height of h above a inclined plane as shown. if the friction coefficient between rope and the plane is μ, find the minimum and maximum length of that part of the rope which can lie on the plane. (L>h)
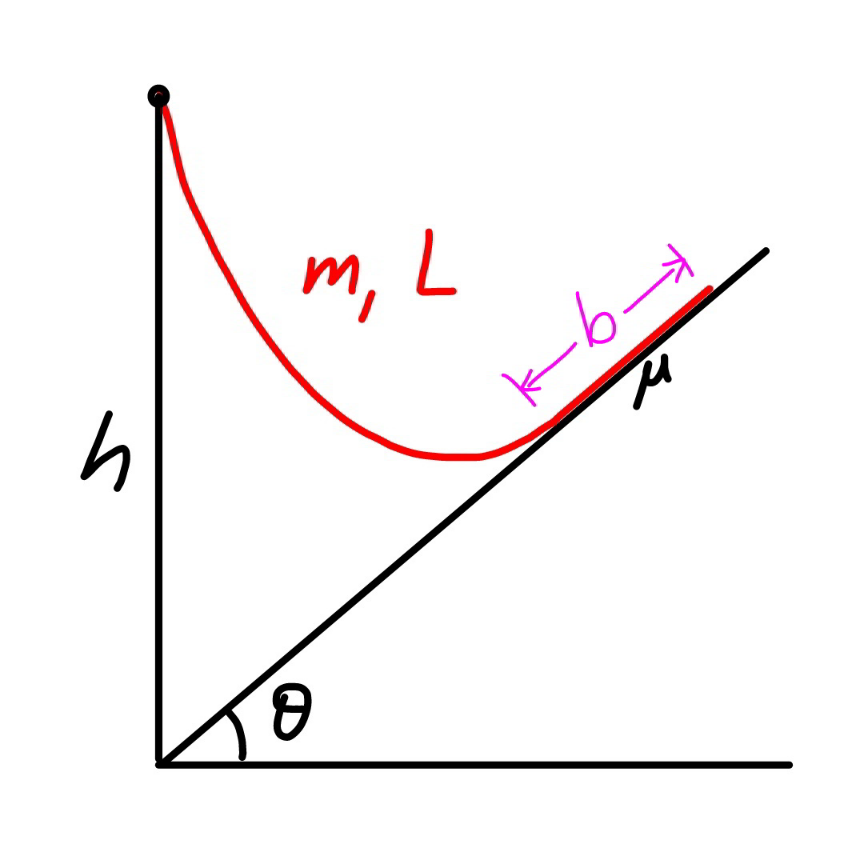
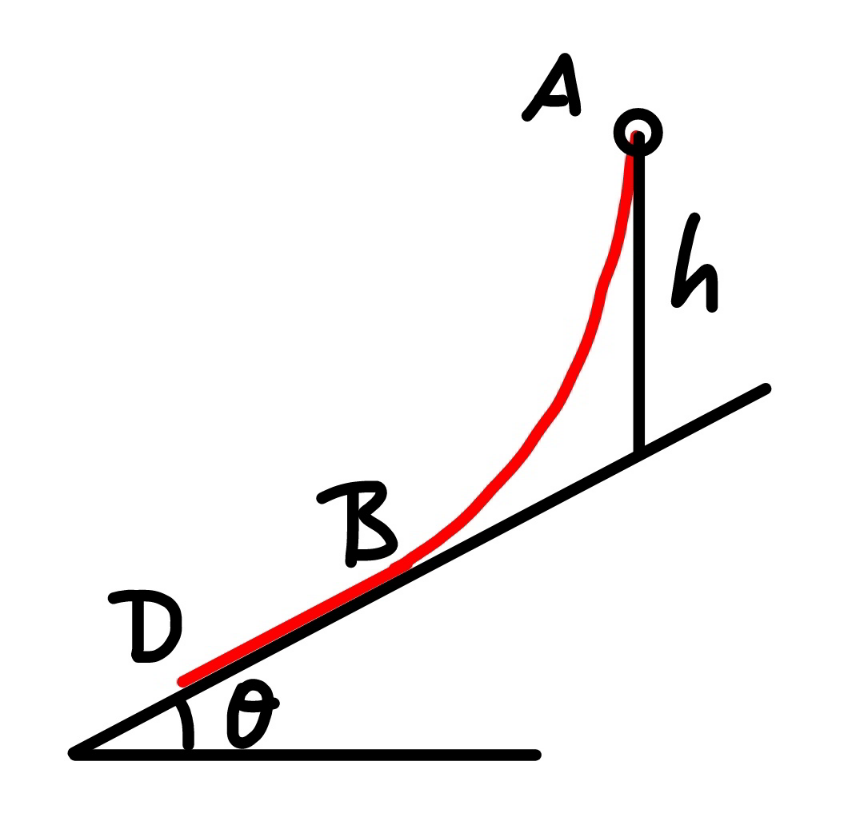
$${an}\:{uniform}\:{thin}\:{rope}\:{with}\:{length}\:{L} \\ $$$${is}\:{hanging}\:{at}\:{one}\:{end}\:{at}\:{a}\:{height}\:{of}\:{h}\: \\ $$$${above}\:{a}\:{inclined}\:{plane}\:{as}\:{shown}.\: \\ $$$${if}\:{the}\:{friction}\:{coefficient}\:{between}\: \\ $$$${rope}\:{and}\:{the}\:{plane}\:{is}\:\mu,\:{find}\:{the} \\ $$$${minimum}\:{and}\:{maximum}\:{length}\:{of}\: \\ $$$${that}\:{part}\:{of}\:{the}\:{rope}\:{which}\:{can}\:{lie}\:{on}\: \\ $$$${the}\:{plane}. \\ $$$$\left({L}>{h}\right) \\ $$
Answered by aleks041103 last updated on 28/May/22
Commented by aleks041103 last updated on 28/May/22
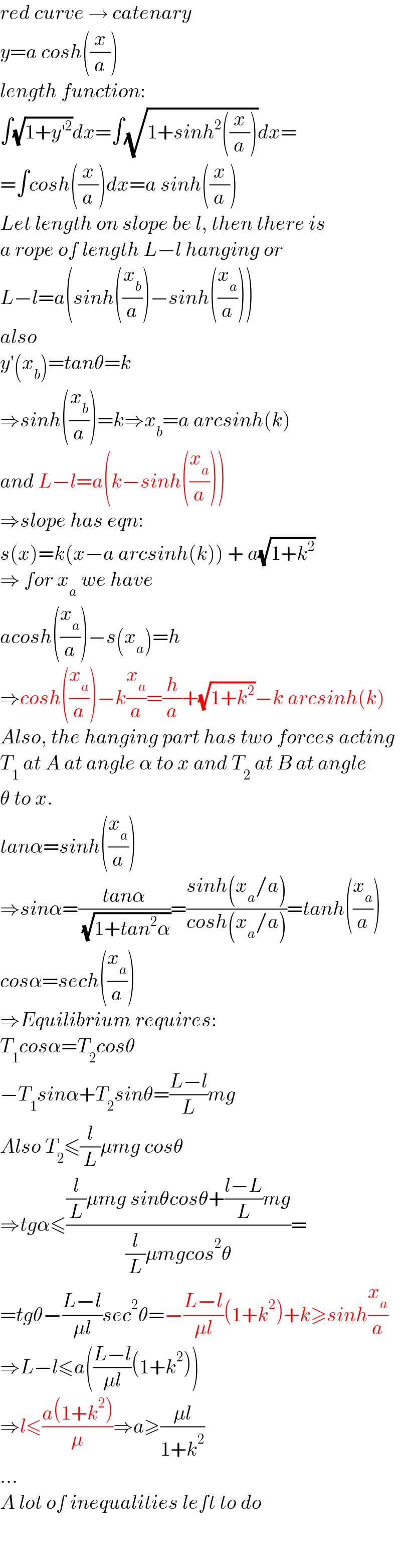
red curve → catenary y=a cosh((x/a)) length function: ∫(√(1+y′^2 ))dx=∫(√(1+sinh^2 ((x/a))))dx= =∫cosh((x/a))dx=a sinh((x/a)) Let length on slope be l, then there is a rope of length L−l hanging or L−l=a(sinh((x_b /a))−sinh((x_a /a))) also y′(x_b )=tanθ=k ⇒sinh((x_b /a))=k⇒x_b =a arcsinh(k) and L−l=a(k−sinh((x_a /a))) ⇒slope has eqn: s(x)=k(x−a arcsinh(k)) + a(√(1+k^2 )) ⇒ for x_a we have acosh((x_a /a))−s(x_a )=h ⇒cosh((x_a /a))−k(x_a /a)=(h/a)+(√(1+k^2 ))−k arcsinh(k) Also, the hanging part has two forces acting T_1 at A at angle α to x and T_2 at B at angle θ to x. tanα=sinh((x_a /a)) ⇒sinα=((tanα)/( (√(1+tan^2 α))))=((sinh(x_a /a))/(cosh(x_a /a)))=tanh((x_a /a)) cosα=sech((x_a /a)) ⇒Equilibrium requires: T_1 cosα=T_2 cosθ −T_1 sinα+T_2 sinθ=((L−l)/L)mg Also T_2 ≤(l/L)μmg cosθ ⇒tgα≤(((l/L)μmg sinθcosθ+((l−L)/L)mg)/((l/L)μmgcos^2 θ))= =tgθ−((L−l)/(μl))sec^2 θ=−((L−l)/(μl))(1+k^2 )+k≥sinh(x_a /a) ⇒L−l≤a(((L−l)/(μl))(1+k^2 )) ⇒l≤((a(1+k^2 ))/μ)⇒a≥((μl)/(1+k^2 )) ... A lot of inequalities left to do
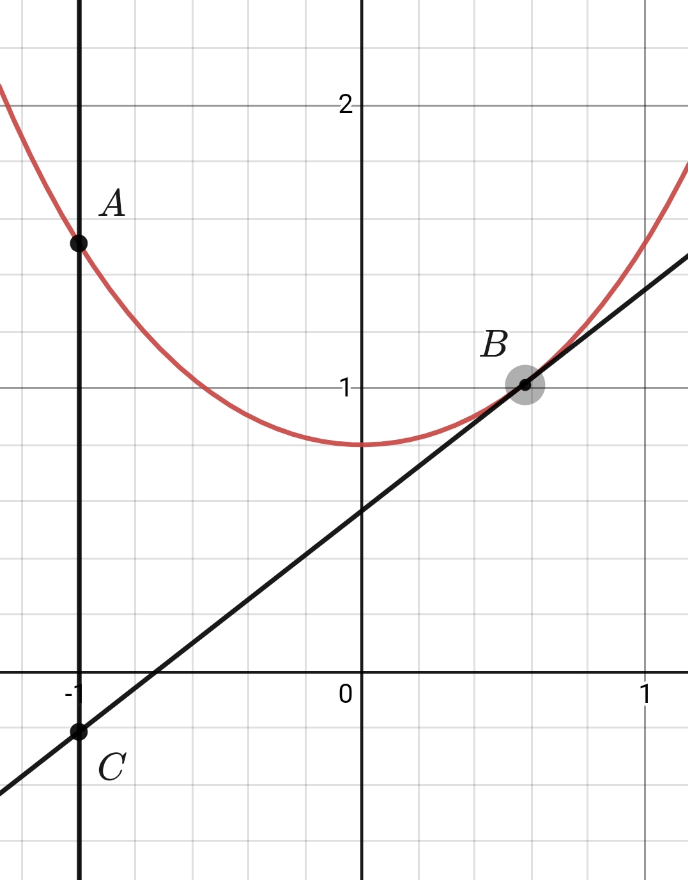
$${red}\:{curve}\:\rightarrow\:{catenary} \\ $$$${y}={a}\:{cosh}\left(\frac{{x}}{{a}}\right) \\ $$$${length}\:{function}: \\ $$$$\int\sqrt{\mathrm{1}+{y}'^{\mathrm{2}} }{dx}=\int\sqrt{\mathrm{1}+{sinh}^{\mathrm{2}} \left(\frac{{x}}{{a}}\right)}{dx}= \\ $$$$=\int{cosh}\left(\frac{{x}}{{a}}\right){dx}={a}\:{sinh}\left(\frac{{x}}{{a}}\right) \\ $$$${Let}\:{length}\:{on}\:{slope}\:{be}\:{l},\:{then}\:{there}\:{is} \\ $$$${a}\:{rope}\:{of}\:{length}\:{L}−{l}\:{hanging}\:{or} \\ $$$${L}−{l}={a}\left({sinh}\left(\frac{{x}_{{b}} }{{a}}\right)−{sinh}\left(\frac{{x}_{{a}} }{{a}}\right)\right) \\ $$$${also} \\ $$$${y}'\left({x}_{{b}} \right)={tan}\theta={k} \\ $$$$\Rightarrow{sinh}\left(\frac{{x}_{{b}} }{{a}}\right)={k}\Rightarrow{x}_{{b}} ={a}\:{arcsinh}\left({k}\right) \\ $$$${and}\:{L}−{l}={a}\left({k}−{sinh}\left(\frac{{x}_{{a}} }{{a}}\right)\right) \\ $$$$\Rightarrow{slope}\:{has}\:{eqn}: \\ $$$${s}\left({x}\right)={k}\left({x}−{a}\:{arcsinh}\left({k}\right)\right)\:+\:{a}\sqrt{\mathrm{1}+{k}^{\mathrm{2}} } \\ $$$$\Rightarrow\:{for}\:{x}_{{a}} \:{we}\:{have} \\ $$$${acosh}\left(\frac{{x}_{{a}} }{{a}}\right)−{s}\left({x}_{{a}} \right)={h} \\ $$$$\Rightarrow{cosh}\left(\frac{{x}_{{a}} }{{a}}\right)−{k}\frac{{x}_{{a}} }{{a}}=\frac{{h}}{{a}}+\sqrt{\mathrm{1}+{k}^{\mathrm{2}} }−{k}\:{arcsinh}\left({k}\right) \\ $$$${Also},\:{the}\:{hanging}\:{part}\:{has}\:{two}\:{forces}\:{acting} \\ $$$${T}_{\mathrm{1}} \:{at}\:{A}\:{at}\:{angle}\:\alpha\:{to}\:{x}\:{and}\:{T}_{\mathrm{2}} \:{at}\:{B}\:{at}\:{angle} \\ $$$$\theta\:{to}\:{x}. \\ $$$${tan}\alpha={sinh}\left(\frac{{x}_{{a}} }{{a}}\right) \\ $$$$\Rightarrow{sin}\alpha=\frac{{tan}\alpha}{\:\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \alpha}}=\frac{{sinh}\left({x}_{{a}} /{a}\right)}{{cosh}\left({x}_{{a}} /{a}\right)}={tanh}\left(\frac{{x}_{{a}} }{{a}}\right) \\ $$$${cos}\alpha={sech}\left(\frac{{x}_{{a}} }{{a}}\right) \\ $$$$\Rightarrow{Equilibrium}\:{requires}: \\ $$$${T}_{\mathrm{1}} {cos}\alpha={T}_{\mathrm{2}} {cos}\theta \\ $$$$−{T}_{\mathrm{1}} {sin}\alpha+{T}_{\mathrm{2}} {sin}\theta=\frac{{L}−{l}}{{L}}{mg} \\ $$$${Also}\:{T}_{\mathrm{2}} \leqslant\frac{{l}}{{L}}\mu{mg}\:{cos}\theta \\ $$$$\Rightarrow{tg}\alpha\leqslant\frac{\frac{{l}}{{L}}\mu{mg}\:{sin}\theta{cos}\theta+\frac{{l}−{L}}{{L}}{mg}}{\frac{{l}}{{L}}\mu{mgcos}^{\mathrm{2}} \theta}= \\ $$$$={tg}\theta−\frac{{L}−{l}}{\mu{l}}{sec}^{\mathrm{2}} \theta=−\frac{{L}−{l}}{\mu{l}}\left(\mathrm{1}+{k}^{\mathrm{2}} \right)+{k}\geqslant{sinh}\frac{{x}_{{a}} }{{a}} \\ $$$$\Rightarrow{L}−{l}\leqslant{a}\left(\frac{{L}−{l}}{\mu{l}}\left(\mathrm{1}+{k}^{\mathrm{2}} \right)\right) \\ $$$$\Rightarrow{l}\leqslant\frac{{a}\left(\mathrm{1}+{k}^{\mathrm{2}} \right)}{\mu}\Rightarrow{a}\geqslant\frac{\mu{l}}{\mathrm{1}+{k}^{\mathrm{2}} } \\ $$$$… \\ $$$${A}\:{lot}\:{of}\:{inequalities}\:{left}\:{to}\:{do} \\ $$$$ \\ $$$$ \\ $$
Commented by mr W last updated on 29/May/22
thanks for the solution sir!
$${thanks}\:{for}\:{the}\:{solution}\:{sir}! \\ $$
Answered by mr W last updated on 29/May/22
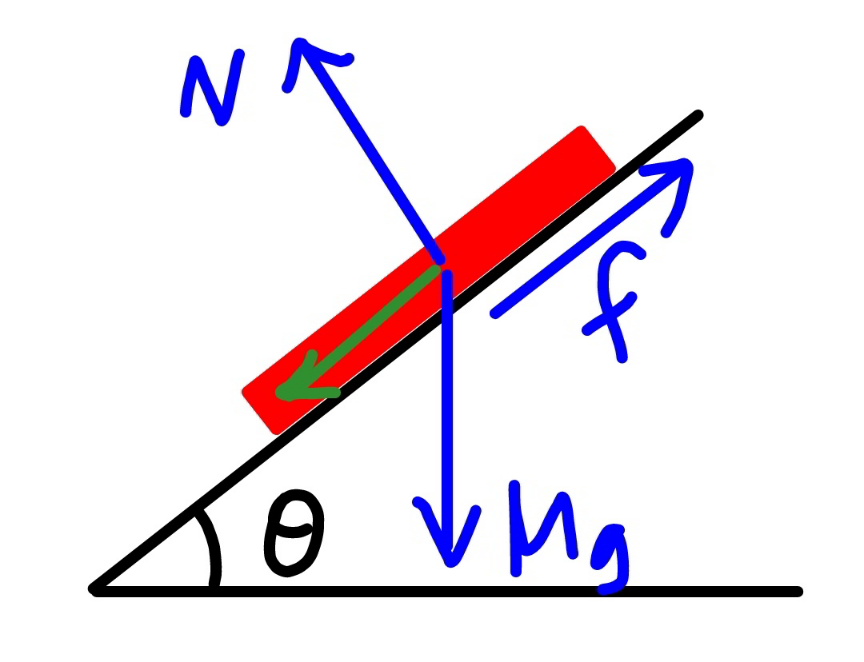
Commented by mr W last updated on 29/May/22
let′s have a look at an object on an inclined plane. such that the object is in equilibrium on such a slope, i.e. such that it doesn′t slide down, a friction force f must act between the object and the slope as shown. the friction coefficient between them defines actually the maximal possible friction force between them. f=μN with 0≤μ≤μ_(nax) . though we speak of friction coefficient μ, but actually we mean the maximal possible friction coefficient μ_(max) . the actual friction coefficient μ must fulfull 0≤μ≤μ_(max) . in following with μ i′ll denote the actual friction coefficient between rope and slope. f=μN N=Mg cos θ such that the object doesn′t slide down, f−Mg sin θ=0 μMg cos θ−Mg sin θ=0 μ cos θ−sin θ=0 μ=((sin θ)/(cos θ))=tan θ≤μ_(max) if the friction coefficient μ_(nax) is smaller than tan θ, an object can not be in equilibrium on the slope. since in our case a part of the rope can lie on the slope, we must have μ_(max) ≥tan θ.
$${let}'{s}\:{have}\:{a}\:{look}\:{at}\:{an}\:{object}\:{on}\:{an} \\ $$$${inclined}\:{plane}. \\ $$$${such}\:{that}\:{the}\:{object}\:{is}\:{in}\:{equilibrium} \\ $$$${on}\:{such}\:{a}\:{slope},\:{i}.{e}.\:{such}\:{that}\:{it} \\ $$$${doesn}'{t}\:{slide}\:{down},\:{a}\:{friction}\:{force}\:{f} \\ $$$${must}\:{act}\:{between}\:{the}\:{object}\:{and}\:{the} \\ $$$${slope}\:{as}\:{shown}.\:{the}\:{friction}\:{coefficient} \\ $$$${between}\:{them}\:{defines}\:{actually}\:{the}\: \\ $$$${maximal}\:{possible}\:{friction}\:{force}\: \\ $$$${between}\:{them}. \\ $$$${f}=\mu{N}\:{with}\:\mathrm{0}\leqslant\mu\leqslant\mu_{{nax}} . \\ $$$${though}\:{we}\:{speak}\:{of}\:{friction} \\ $$$${coefficient}\:\mu,\:{but}\:{actually}\:{we}\:{mean} \\ $$$${the}\:{maximal}\:{possible}\:{friction} \\ $$$${coefficient}\:\mu_{{max}} .\:{the}\:{actual}\:{friction} \\ $$$${coefficient}\:\mu\:{must}\:{fulfull}\:\mathrm{0}\leqslant\mu\leqslant\mu_{{max}} . \\ $$$${in}\:{following}\:{with}\:\mu\:{i}'{ll}\:{denote}\:{the} \\ $$$${actual}\:{friction}\:{coefficient}\:{between} \\ $$$${rope}\:{and}\:{slope}. \\ $$$${f}=\mu{N} \\ $$$${N}={Mg}\:\mathrm{cos}\:\theta \\ $$$${such}\:{that}\:{the}\:{object}\:{doesn}'{t}\:{slide} \\ $$$${down},\: \\ $$$${f}−{Mg}\:\mathrm{sin}\:\theta=\mathrm{0} \\ $$$$\mu{Mg}\:\mathrm{cos}\:\theta−{Mg}\:\mathrm{sin}\:\theta=\mathrm{0} \\ $$$$\mu\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta=\mathrm{0} \\ $$$$\mu=\frac{\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}=\mathrm{tan}\:\theta\leqslant\mu_{{max}} \\ $$$${if}\:{the}\:{friction}\:{coefficient}\:\mu_{{nax}} \:{is} \\ $$$${smaller}\:{than}\:\mathrm{tan}\:\theta,\:{an}\:{object}\:{can}\:{not} \\ $$$${be}\:{in}\:{equilibrium}\:{on}\:{the}\:{slope}. \\ $$$${since}\:{in}\:{our}\:{case}\:{a}\:{part}\:{of}\:{the}\:{rope} \\ $$$${can}\:{lie}\:{on}\:{the}\:{slope},\:{we}\:{must}\:{have}\: \\ $$$$\mu_{{max}} \geqslant\mathrm{tan}\:\theta. \\ $$
Commented by mr W last updated on 29/May/22
Commented by mr W last updated on 29/May/22
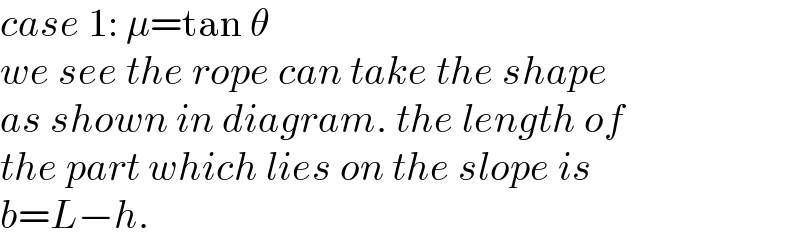
case 1: μ=tan θ we see the rope can take the shape as shown in diagram. the length of the part which lies on the slope is b=L−h.
$${case}\:\mathrm{1}:\:\mu=\mathrm{tan}\:\theta \\ $$$${we}\:{see}\:{the}\:{rope}\:{can}\:{take}\:{the}\:{shape} \\ $$$${as}\:{shown}\:{in}\:{diagram}.\:{the}\:{length}\:{of} \\ $$$${the}\:{part}\:{which}\:{lies}\:{on}\:{the}\:{slope}\:{is} \\ $$$${b}={L}−{h}. \\ $$
Commented by mr W last updated on 29/May/22
Commented by mr W last updated on 29/May/22
case 2: μ>tan θ the friction force f is large enough so that it can even allow an addition tension force between the two parts of the rope.
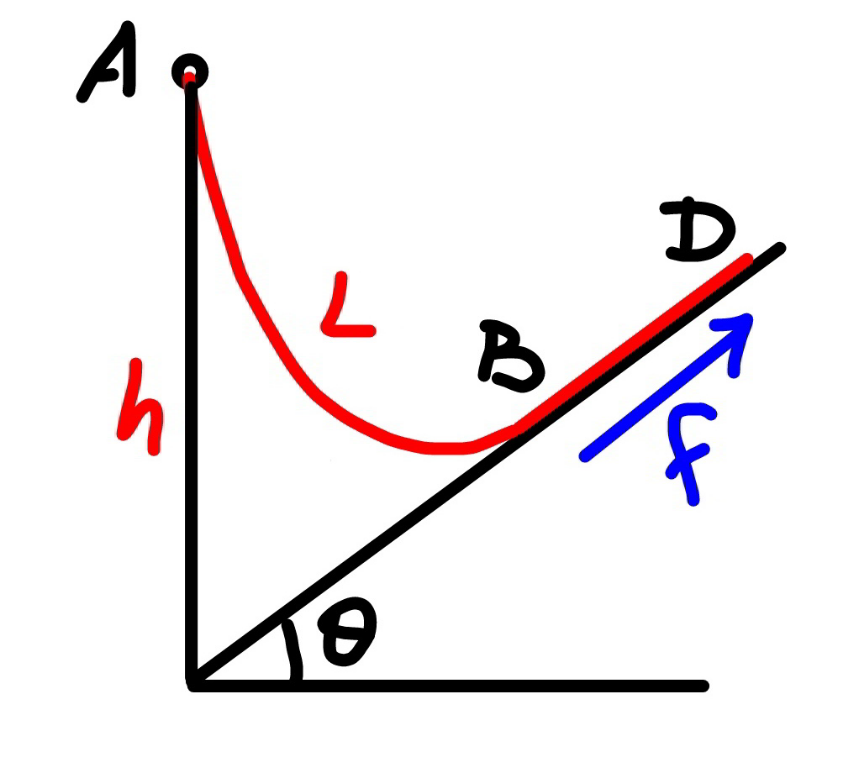
$${case}\:\mathrm{2}:\:\mu>\mathrm{tan}\:\theta \\ $$$${the}\:{friction}\:{force}\:{f}\:{is}\:{large}\:{enough} \\ $$$${so}\:{that}\:{it}\:{can}\:{even}\:{allow}\:{an} \\ $$$${addition}\:{tension}\:{force}\:{between}\:{the} \\ $$$${two}\:{parts}\:{of}\:{the}\:{rope}.\: \\ $$
Commented by mr W last updated on 29/May/22
Commented by mr W last updated on 29/May/22
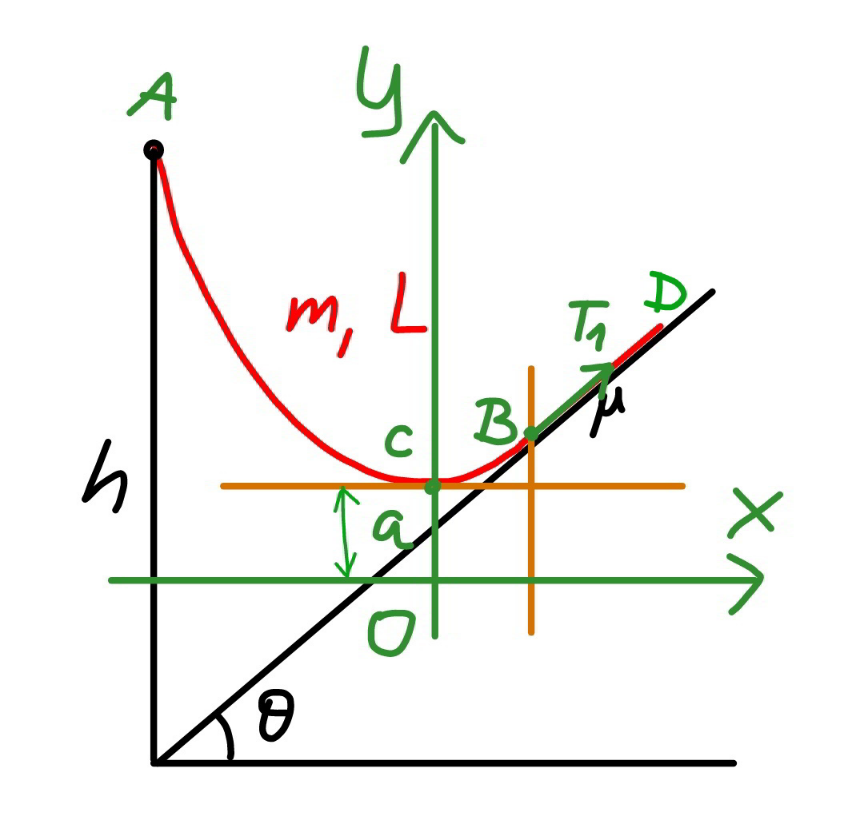
say the length of the rope part which lies on the inclined plane is b. ρ=(m/L) the friction force between rope and the slope is f. f=μρgb cos θ with tan θ<μ≤μ_(max) tension in the rope at point B: T_1 =f−ρgb sin θ=(μ cos θ−sin θ)ρgb let μ′=μ cos θ−sin θ T_1 =μ′ρgb T_0 =T_1 cos θ=μ′ρgb cos θ define a=(T_0 /(ρg))=μ′b cos θ the hanging rope from point A to B is part of a catenary. w.r.t. the coordinate system as shown, y=a cosh (x/a) y′=sinh (x/a) s=a sinh (x/a) tan θ=sinh (x_B /a) ⇒(x_B /a)=sinh^(−1) (tan θ) s_1 =CB^(⌢) =a sinh (x_B /a)=a tan θ AC^(⌢) =L−b−s_1 =a sinh (x_A /a) L−b−a tan θ=a sinh (x_A /a) ⇒(x_A /a)=sinh^(−1) (((L−b)/a)−tan θ) y_A −y_B =h−(x_A +x_B ) tan θ a cosh (x_A /a)−a cosh (x_B /a)=h−(x_A +x_B ) tan θ cosh (x_A /a)−cosh (x_B /a)=(h/a)−((x_A /a)+(x_B /a)) tan θ cosh [sinh^(−1) (((L−b)/a)−tan θ)]−cosh [sinh^(−1) (tan θ)]=(h/a)−[sinh^(−1) (((L−b)/a)−tan θ)+sinh^(−1) (tan θ)] tan θ let (b/L)=(1/λ) cosh [sinh^(−1) (((λ−1)/(μ′ cos θ))−tan θ)]−cosh [sinh^(−1) (tan θ)]=((λh)/(μ′L cos θ))−[sinh^(−1) (((λ−1)/(μ′ cos θ))−tan θ)+sinh^(−1) (tan θ)] tan θ ⇒[sinh^(−1) (((𝛌−1)/(𝛍′ cos 𝛉))−tan 𝛉)+sinh^(−1) (tan 𝛉)]sin 𝛉=1+((𝛌h)/(𝛍′L))−(√(1+(((𝛌−1)/(𝛍′)))^2 −2(((𝛌−1)/(𝛍′))) sin 𝛉)) this equation shows the relationship between λ and the actual friction coefficient μ (tan θ<μ≤μ_(max) ). generally this relationship looks like as shown in the diagram below. example: h=3m, L=5m, θ=30°, μ_(max) =1.5 ⇒(b_(min) /L)=0.33202 at μ=1.5 ⇒(b_(max) /L)=0.43165 at μ=0.7
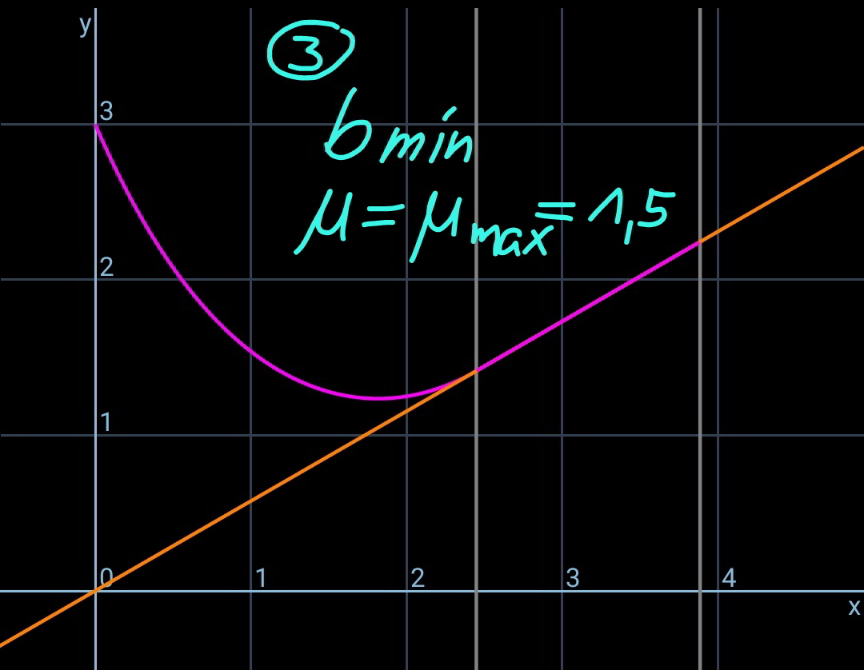
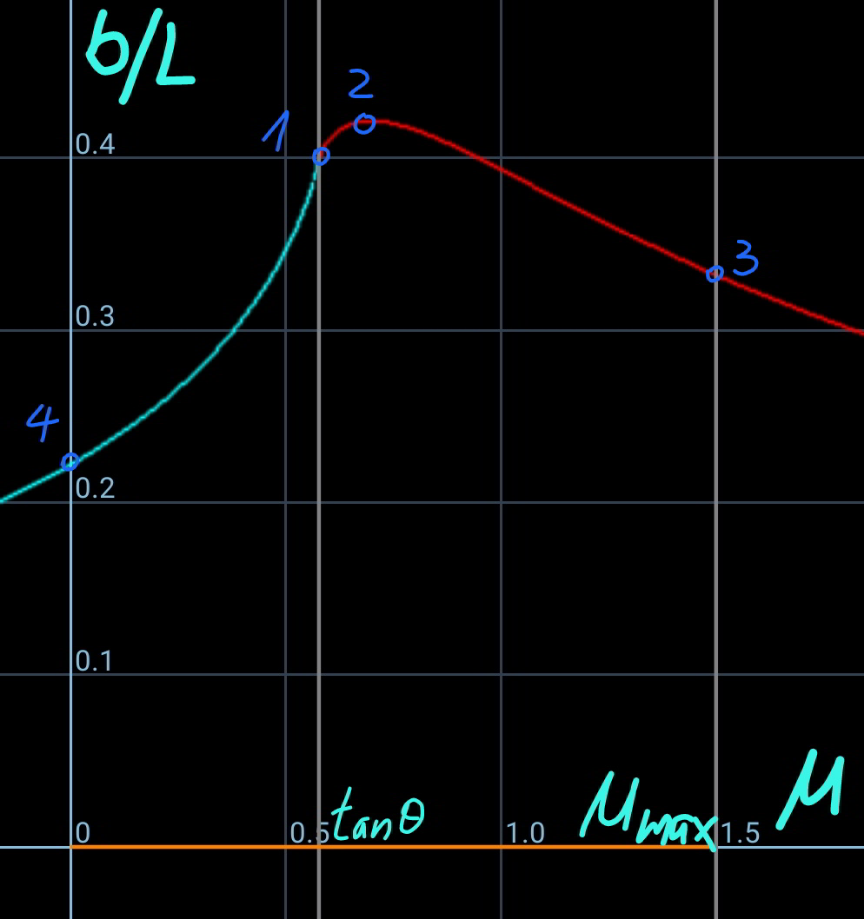
$${say}\:{the}\:{length}\:{of}\:{the}\:{rope}\:{part}\:{which} \\ $$$${lies}\:{on}\:{the}\:{inclined}\:{plane}\:{is}\:{b}. \\ $$$$\rho=\frac{{m}}{{L}} \\ $$$${the}\:{friction}\:{force}\:{between}\:{rope}\:{and} \\ $$$${the}\:{slope}\:{is}\:{f}. \\ $$$${f}=\mu\rho{gb}\:\mathrm{cos}\:\theta\:{with}\:\mathrm{tan}\:\theta<\mu\leqslant\mu_{{max}} \\ $$$${tension}\:{in}\:{the}\:{rope}\:{at}\:{point}\:{B}: \\ $$$${T}_{\mathrm{1}} ={f}−\rho{gb}\:\mathrm{sin}\:\theta=\left(\mu\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)\rho{gb} \\ $$$${let}\:\mu'=\mu\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta \\ $$$${T}_{\mathrm{1}} =\mu'\rho{gb} \\ $$$${T}_{\mathrm{0}} ={T}_{\mathrm{1}} \:\mathrm{cos}\:\theta=\mu'\rho{gb}\:\mathrm{cos}\:\theta \\ $$$${define}\:{a}=\frac{{T}_{\mathrm{0}} }{\rho{g}}=\mu'{b}\:\mathrm{cos}\:\theta \\ $$$${the}\:{hanging}\:{rope}\:{from}\:{point}\:{A}\:{to}\:{B}\: \\ $$$${is}\:{part}\:{of}\:{a}\:{catenary}.\:{w}.{r}.{t}.\:{the} \\ $$$${coordinate}\:{system}\:{as}\:{shown}, \\ $$$${y}={a}\:\mathrm{cosh}\:\frac{{x}}{{a}} \\ $$$${y}'=\mathrm{sinh}\:\frac{{x}}{{a}} \\ $$$${s}={a}\:\mathrm{sinh}\:\frac{{x}}{{a}} \\ $$$$ \\ $$$$\mathrm{tan}\:\theta=\mathrm{sinh}\:\frac{{x}_{{B}} }{{a}}\:\Rightarrow\frac{{x}_{{B}} }{{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right) \\ $$$${s}_{\mathrm{1}} =\overset{\frown} {{CB}}={a}\:\mathrm{sinh}\:\frac{{x}_{{B}} }{{a}}={a}\:\mathrm{tan}\:\theta \\ $$$$\overset{\frown} {{AC}}={L}−{b}−{s}_{\mathrm{1}} ={a}\:\mathrm{sinh}\:\frac{{x}_{{A}} }{{a}} \\ $$$${L}−{b}−{a}\:\mathrm{tan}\:\theta={a}\:\mathrm{sinh}\:\frac{{x}_{{A}} }{{a}} \\ $$$$\Rightarrow\frac{{x}_{{A}} }{{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{{L}−{b}}{{a}}−\mathrm{tan}\:\theta\right) \\ $$$${y}_{{A}} −{y}_{{B}} ={h}−\left({x}_{{A}} +{x}_{{B}} \right)\:\mathrm{tan}\:\theta \\ $$$${a}\:\mathrm{cosh}\:\frac{{x}_{{A}} }{{a}}−{a}\:\mathrm{cosh}\:\frac{{x}_{{B}} }{{a}}={h}−\left({x}_{{A}} +{x}_{{B}} \right)\:\mathrm{tan}\:\theta \\ $$$$\mathrm{cosh}\:\frac{{x}_{{A}} }{{a}}−\mathrm{cosh}\:\frac{{x}_{{B}} }{{a}}=\frac{{h}}{{a}}−\left(\frac{{x}_{{A}} }{{a}}+\frac{{x}_{{B}} }{{a}}\right)\:\mathrm{tan}\:\theta \\ $$$$\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{{L}−{b}}{{a}}−\mathrm{tan}\:\theta\right)\right]−\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right)\right]=\frac{{h}}{{a}}−\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{{L}−{b}}{{a}}−\mathrm{tan}\:\theta\right)+\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right)\right]\:\mathrm{tan}\:\theta \\ $$$${let}\:\frac{{b}}{{L}}=\frac{\mathrm{1}}{\lambda} \\ $$$$\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{\lambda−\mathrm{1}}{\mu'\:\mathrm{cos}\:\theta}−\mathrm{tan}\:\theta\right)\right]−\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right)\right]=\frac{\lambda{h}}{\mu'{L}\:\mathrm{cos}\:\theta}−\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{\lambda−\mathrm{1}}{\mu'\:\mathrm{cos}\:\theta}−\mathrm{tan}\:\theta\right)+\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right)\right]\:\mathrm{tan}\:\theta \\ $$$$\Rightarrow\left[\boldsymbol{\mathrm{sinh}}^{−\mathrm{1}} \:\left(\frac{\boldsymbol{\lambda}−\mathrm{1}}{\boldsymbol{\mu}'\:\boldsymbol{\mathrm{cos}}\:\boldsymbol{\theta}}−\boldsymbol{\mathrm{tan}}\:\boldsymbol{\theta}\right)+\boldsymbol{\mathrm{sinh}}^{−\mathrm{1}} \:\left(\boldsymbol{\mathrm{tan}}\:\boldsymbol{\theta}\right)\right]\boldsymbol{\mathrm{sin}}\:\boldsymbol{\theta}=\mathrm{1}+\frac{\boldsymbol{\lambda{h}}}{\boldsymbol{\mu}'\boldsymbol{{L}}}−\sqrt{\mathrm{1}+\left(\frac{\boldsymbol{\lambda}−\mathrm{1}}{\boldsymbol{\mu}'}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{\boldsymbol{\lambda}−\mathrm{1}}{\boldsymbol{\mu}'}\right)\:\boldsymbol{\mathrm{sin}}\:\boldsymbol{\theta}} \\ $$$${this}\:{equation}\:{shows}\:{the}\:{relationship} \\ $$$${between}\:\lambda\:{and}\:{the}\:{actual}\:{friction} \\ $$$${coefficient}\:\mu\:\left(\mathrm{tan}\:\theta<\mu\leqslant\mu_{{max}} \right). \\ $$$${generally}\:{this}\:{relationship}\:{looks}\:{like} \\ $$$${as}\:{shown}\:{in}\:{the}\:{diagram}\:{below}. \\ $$$$ \\ $$$${example}: \\ $$$${h}=\mathrm{3}{m},\:{L}=\mathrm{5}{m},\:\theta=\mathrm{30}°,\:\mu_{{max}} =\mathrm{1}.\mathrm{5} \\ $$$$\Rightarrow\frac{{b}_{{min}} }{{L}}=\mathrm{0}.\mathrm{33202}\:{at}\:\mu=\mathrm{1}.\mathrm{5} \\ $$$$\Rightarrow\frac{{b}_{{max}} }{{L}}=\mathrm{0}.\mathrm{43165}\:{at}\:\mu=\mathrm{0}.\mathrm{7} \\ $$
Commented by mr W last updated on 29/May/22
Commented by mr W last updated on 29/May/22
point 1: this is the case 1 with μ=tan θ and (b/L)=((L−h)/L)=1−(h/L)=0.4 point 3: this is the situation when the friction reaches its maximum and the part of rope which lies on the rope is the minimum. point 2: this is the situation when the part of rope on the slope has its maximum length. we can not put more rope on the slope and still keep it in equilibrium.
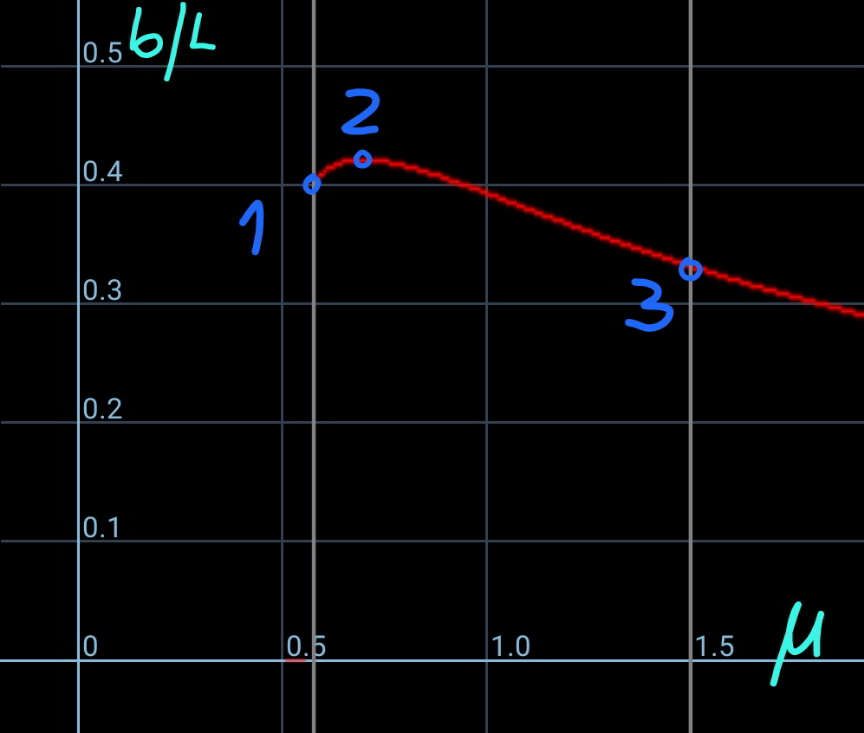
$${point}\:\mathrm{1}:\: \\ $$$${this}\:{is}\:{the}\:{case}\:\mathrm{1}\:{with} \\ $$$$\mu=\mathrm{tan}\:\theta\:{and}\:\frac{{b}}{{L}}=\frac{{L}−{h}}{{L}}=\mathrm{1}−\frac{{h}}{{L}}=\mathrm{0}.\mathrm{4} \\ $$$${point}\:\mathrm{3}:\: \\ $$$${this}\:{is}\:{the}\:{situation}\:{when}\:{the}\:{friction} \\ $$$${reaches}\:{its}\:{maximum}\:{and}\:{the}\:{part}\:{of} \\ $$$${rope}\:{which}\:{lies}\:{on}\:{the}\:{rope}\:{is}\:{the} \\ $$$${minimum}. \\ $$$${point}\:\mathrm{2}: \\ $$$${this}\:{is}\:{the}\:{situation}\:{when}\:{the}\:{part}\:{of} \\ $$$${rope}\:{on}\:{the}\:{slope}\:{has}\:{its}\:{maximum} \\ $$$${length}.\:{we}\:{can}\:{not}\:{put}\:{more}\:{rope}\:{on} \\ $$$${the}\:{slope}\:{and}\:{still}\:{keep}\:{it}\:{in}\:{equilibrium}. \\ $$
Commented by mr W last updated on 29/May/22
Commented by mr W last updated on 29/May/22
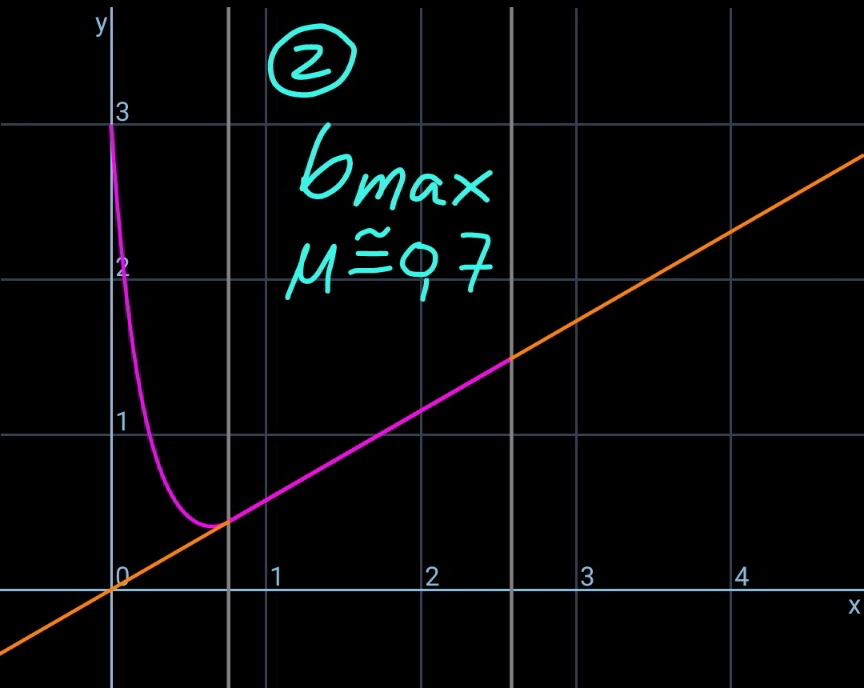
Commented by mr W last updated on 29/May/22
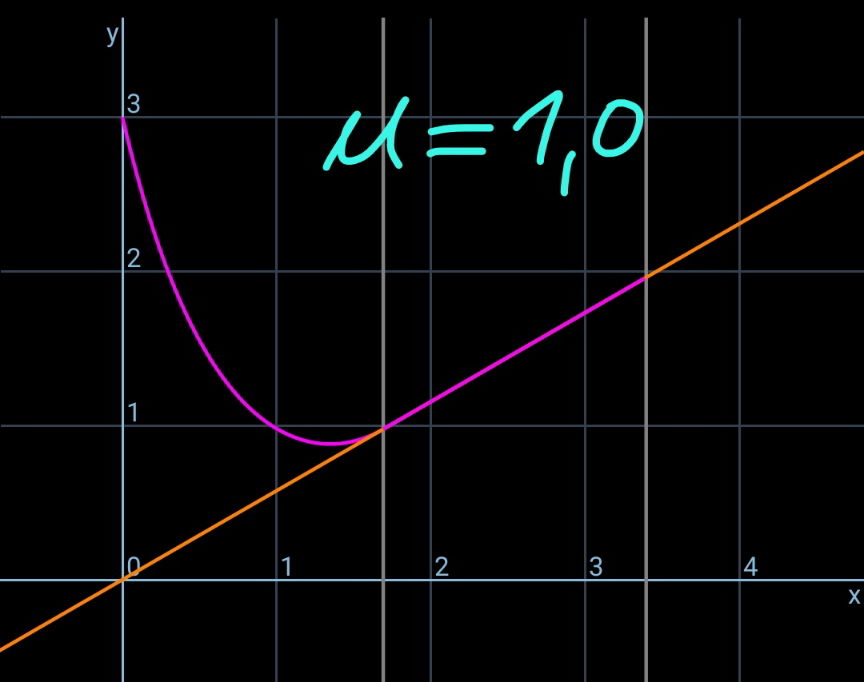
Commented by mr W last updated on 29/May/22
Commented by mr W last updated on 29/May/22
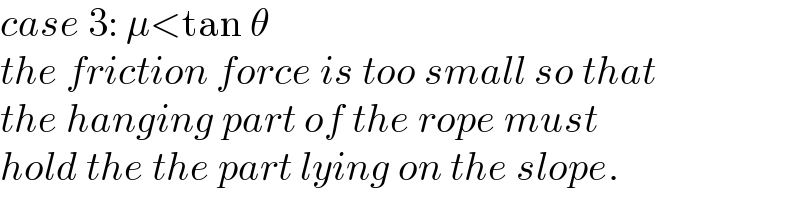
case 3: μ<tan θ the friction force is too small so that the hanging part of the rope must hold the the part lying on the slope.
$${case}\:\mathrm{3}:\:\mu<\mathrm{tan}\:\theta \\ $$$${the}\:{friction}\:{force}\:{is}\:{too}\:{small}\:{so}\:{that} \\ $$$${the}\:{hanging}\:{part}\:{of}\:{the}\:{rope}\:{must}\: \\ $$$${hold}\:{the}\:{the}\:{part}\:{lying}\:{on}\:{the}\:{slope}. \\ $$
Commented by mr W last updated on 29/May/22
Commented by mr W last updated on 29/May/22
Commented by mr W last updated on 29/May/22
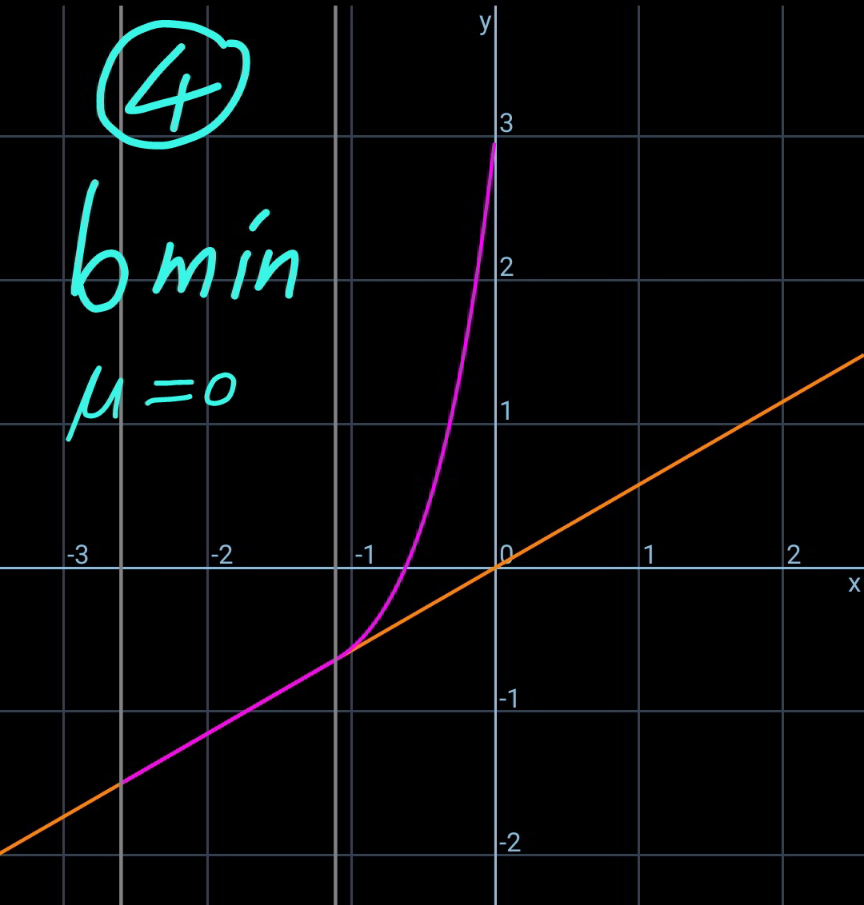
say the length of the rope part which lies on the inclined plane is b. the friction force between rope and the slope is f. f=μρgb cos θ with 0≤μ<tan θ tension in the rope at point B: T_1 =ρgb sin θ−f=(sin θ−μ cos θ)ρgb let μ′=μ cos θ−sin θ T_1 =−μ′ρgb T_0 =T_1 cos θ=−μ′ρgb cos θ define a=(T_0 /(ρg))=−μ′b cos θ the hanging rope from point A to B is part of a catenary. w.r.t. the coordinate system as shown, y=a cosh (x/a) y′=sinh (x/a) s=a sinh (x/a) tan θ=sinh (x_B /a) ⇒(x_B /a)=sinh^(−1) (tan θ) s_1 =CB^(⌢) =a sinh (x_B /a)=a tan θ AC^(⌢) =L−b+s_1 =a sinh (x_A /a) L−b+a tan θ=a sinh (x_A /a) ⇒(x_A /a)=sinh^(−1) (((L−b)/a)+tan θ) y_A −y_B =h+(x_A −x_B ) tan θ a cosh (x_A /a)−a cosh (x_B /a)=h+(x_A −x_B ) tan θ cosh (x_A /a)−cosh (x_B /a)=(h/a)+((x_A /a)−(x_B /a)) tan θ cosh [sinh^(−1) (((L−b)/a)+tan θ)]−cosh [sinh^(−1) (tan θ)]=(h/a)+[sinh^(−1) (((L−b)/a)+tan θ)−sinh^(−1) (tan θ)] tan θ let (b/L)=(1/λ) cosh [sinh^(−1) (−((λ−1)/(μ′ cos θ))+tan θ)]−cosh [sinh^(−1) (tan θ)]=−((λh)/(μ′L cos θ))+[sinh^(−1) (−((λ−1)/(μ′ cos θ))+tan θ)−sinh^(−1) (tan θ)] tan θ ⇒[sinh^(−1) (((𝛌−1)/(𝛍′ cos 𝛉))−tan 𝛉)+sinh^(−1) (tan 𝛉)]sin 𝛉=1− ((𝛌h)/(𝛍′))−(√(1+(((𝛌−1)/(𝛍′)))^2 −2(((𝛌−1)/(𝛍′)))sin 𝛉)) this equation shows the relationship between λ and the actual friction coefficient μ (0≤μ<tan θ). generally this relationship looks like as shown in the diagram below. example: h=3m, L=5m, θ=30°, μ_(max) =1.5 ⇒(b_(min) /L)=0.22196 at μ=0 (point 4) ⇒(b_(max) /L)=0.43165 at μ=0.7 (point 2)
$${say}\:{the}\:{length}\:{of}\:{the}\:{rope}\:{part}\:{which} \\ $$$${lies}\:{on}\:{the}\:{inclined}\:{plane}\:{is}\:{b}. \\ $$$${the}\:{friction}\:{force}\:{between}\:{rope}\:{and} \\ $$$${the}\:{slope}\:{is}\:{f}. \\ $$$${f}=\mu\rho{gb}\:\mathrm{cos}\:\theta\:{with}\:\mathrm{0}\leqslant\mu<\mathrm{tan}\:\theta \\ $$$${tension}\:{in}\:{the}\:{rope}\:{at}\:{point}\:{B}: \\ $$$${T}_{\mathrm{1}} =\rho{gb}\:\mathrm{sin}\:\theta−{f}=\left(\mathrm{sin}\:\theta−\mu\:\mathrm{cos}\:\theta\right)\rho{gb} \\ $$$${let}\:\mu'=\mu\:\mathrm{cos}\:\theta−\mathrm{sin}\:\theta \\ $$$${T}_{\mathrm{1}} =−\mu'\rho{gb} \\ $$$${T}_{\mathrm{0}} ={T}_{\mathrm{1}} \:\mathrm{cos}\:\theta=−\mu'\rho{gb}\:\mathrm{cos}\:\theta \\ $$$${define}\:{a}=\frac{{T}_{\mathrm{0}} }{\rho{g}}=−\mu'{b}\:\mathrm{cos}\:\theta \\ $$$${the}\:{hanging}\:{rope}\:{from}\:{point}\:{A}\:{to}\:{B}\: \\ $$$${is}\:{part}\:{of}\:{a}\:{catenary}.\:{w}.{r}.{t}.\:{the} \\ $$$${coordinate}\:{system}\:{as}\:{shown}, \\ $$$${y}={a}\:\mathrm{cosh}\:\frac{{x}}{{a}} \\ $$$${y}'=\mathrm{sinh}\:\frac{{x}}{{a}} \\ $$$${s}={a}\:\mathrm{sinh}\:\frac{{x}}{{a}} \\ $$$$ \\ $$$$\mathrm{tan}\:\theta=\mathrm{sinh}\:\frac{{x}_{{B}} }{{a}}\:\Rightarrow\frac{{x}_{{B}} }{{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right) \\ $$$${s}_{\mathrm{1}} =\overset{\frown} {{CB}}={a}\:\mathrm{sinh}\:\frac{{x}_{{B}} }{{a}}={a}\:\mathrm{tan}\:\theta \\ $$$$\overset{\frown} {{AC}}={L}−{b}+{s}_{\mathrm{1}} ={a}\:\mathrm{sinh}\:\frac{{x}_{{A}} }{{a}} \\ $$$${L}−{b}+{a}\:\mathrm{tan}\:\theta={a}\:\mathrm{sinh}\:\frac{{x}_{{A}} }{{a}} \\ $$$$\Rightarrow\frac{{x}_{{A}} }{{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{{L}−{b}}{{a}}+\mathrm{tan}\:\theta\right) \\ $$$${y}_{{A}} −{y}_{{B}} ={h}+\left({x}_{{A}} −{x}_{{B}} \right)\:\mathrm{tan}\:\theta \\ $$$${a}\:\mathrm{cosh}\:\frac{{x}_{{A}} }{{a}}−{a}\:\mathrm{cosh}\:\frac{{x}_{{B}} }{{a}}={h}+\left({x}_{{A}} −{x}_{{B}} \right)\:\mathrm{tan}\:\theta \\ $$$$\mathrm{cosh}\:\frac{{x}_{{A}} }{{a}}−\mathrm{cosh}\:\frac{{x}_{{B}} }{{a}}=\frac{{h}}{{a}}+\left(\frac{{x}_{{A}} }{{a}}−\frac{{x}_{{B}} }{{a}}\right)\:\mathrm{tan}\:\theta \\ $$$$\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{{L}−{b}}{{a}}+\mathrm{tan}\:\theta\right)\right]−\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right)\right]=\frac{{h}}{{a}}+\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\frac{{L}−{b}}{{a}}+\mathrm{tan}\:\theta\right)−\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right)\right]\:\mathrm{tan}\:\theta \\ $$$${let}\:\frac{{b}}{{L}}=\frac{\mathrm{1}}{\lambda} \\ $$$$\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(−\frac{\lambda−\mathrm{1}}{\mu'\:\mathrm{cos}\:\theta}+\mathrm{tan}\:\theta\right)\right]−\mathrm{cosh}\:\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right)\right]=−\frac{\lambda{h}}{\mu'{L}\:\mathrm{cos}\:\theta}+\left[\mathrm{sinh}^{−\mathrm{1}} \:\left(−\frac{\lambda−\mathrm{1}}{\mu'\:\mathrm{cos}\:\theta}+\mathrm{tan}\:\theta\right)−\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right)\right]\:\mathrm{tan}\:\theta \\ $$$$\Rightarrow\left[\boldsymbol{\mathrm{sinh}}^{−\mathrm{1}} \:\left(\frac{\boldsymbol{\lambda}−\mathrm{1}}{\boldsymbol{\mu}'\:\boldsymbol{\mathrm{cos}}\:\boldsymbol{\theta}}−\boldsymbol{\mathrm{tan}}\:\boldsymbol{\theta}\right)+\boldsymbol{\mathrm{sinh}}^{−\mathrm{1}} \:\left(\boldsymbol{\mathrm{tan}}\:\boldsymbol{\theta}\right)\right]\boldsymbol{\mathrm{sin}}\:\boldsymbol{\theta}=\mathrm{1}−\:\frac{\boldsymbol{\lambda{h}}}{\boldsymbol{\mu}'}−\sqrt{\mathrm{1}+\left(\frac{\boldsymbol{\lambda}−\mathrm{1}}{\boldsymbol{\mu}'}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{\boldsymbol{\lambda}−\mathrm{1}}{\boldsymbol{\mu}'}\right)\boldsymbol{\mathrm{sin}}\:\boldsymbol{\theta}} \\ $$$${this}\:{equation}\:{shows}\:{the}\:{relationship} \\ $$$${between}\:\lambda\:{and}\:{the}\:{actual}\:{friction} \\ $$$${coefficient}\:\mu\:\left(\mathrm{0}\leqslant\mu<\mathrm{tan}\:\theta\right). \\ $$$${generally}\:{this}\:{relationship}\:{looks}\:{like} \\ $$$${as}\:{shown}\:{in}\:{the}\:{diagram}\:{below}. \\ $$$$ \\ $$$${example}: \\ $$$${h}=\mathrm{3}{m},\:{L}=\mathrm{5}{m},\:\theta=\mathrm{30}°,\:\mu_{{max}} =\mathrm{1}.\mathrm{5} \\ $$$$\Rightarrow\frac{{b}_{{min}} }{{L}}=\mathrm{0}.\mathrm{22196}\:{at}\:\mu=\mathrm{0}\:\left({point}\:\mathrm{4}\right) \\ $$$$\Rightarrow\frac{{b}_{{max}} }{{L}}=\mathrm{0}.\mathrm{43165}\:{at}\:\mu=\mathrm{0}.\mathrm{7}\:\left({point}\:\mathrm{2}\right) \\ $$
Commented by mr W last updated on 30/May/22
Commented by Tawa11 last updated on 06/Oct/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *