Question Number 170663 by kndramaths last updated on 28/May/22
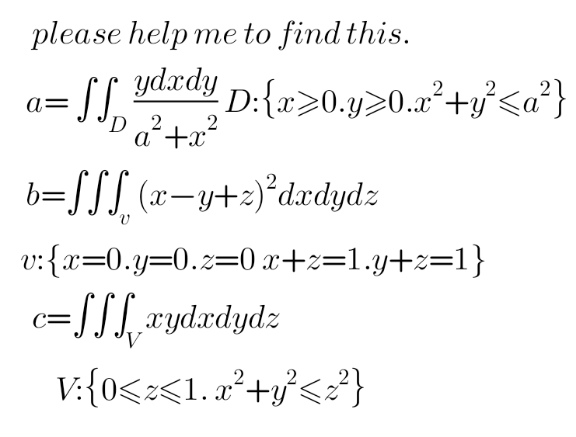
Commented by kaivan.ahmadi last updated on 28/May/22
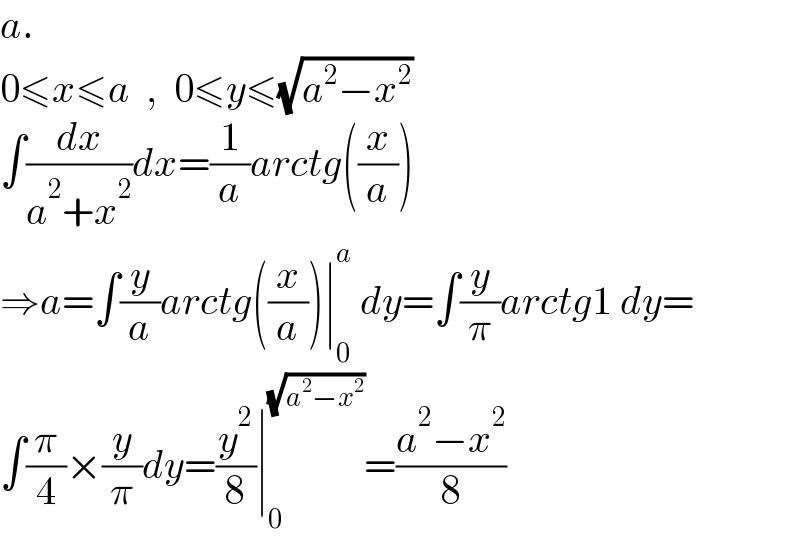
$${a}. \\ $$$$\mathrm{0}\leqslant{x}\leqslant{a}\:\:,\:\:\mathrm{0}\leqslant{y}\leqslant\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$$\int\frac{{dx}}{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{{a}}{arctg}\left(\frac{{x}}{{a}}\right) \\ $$$$\Rightarrow{a}=\int\frac{{y}}{{a}}{arctg}\left(\frac{{x}}{{a}}\right)\mid_{\mathrm{0}} ^{{a}} \:{dy}=\int\frac{{y}}{\pi}{arctg}\mathrm{1}\:{dy}= \\ $$$$\int\frac{\pi}{\mathrm{4}}×\frac{{y}}{\pi}{dy}=\frac{{y}^{\mathrm{2}} }{\mathrm{8}}\mid_{\mathrm{0}} ^{\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }} =\frac{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }{\mathrm{8}} \\ $$
Answered by Mathspace last updated on 29/May/22
![A=∫∫_D (y/(x^2 +a^2 ))dx dy we do the changement x=arcosθ et y=arsinθ ⇒ x^2 +y^2 ≤a^2 ⇒a^2 r^2 ≤a^2 ⇒0≤r≤1 x≥0 and y≥0 ⇒0≤θ≤(π/2) ⇒A=∫∫_(o≤r≤1 and o≤θ≤(π/2)) ((arsinθ)/(a^2 r^2 cos^2 θ+a^2 ))a^2 rdrdθ =a∫∫_(o≤r≤1 and 0≤θ≤(π/2)) ((r^2 sinθ)/(1+r^2 cos^2 θ))dr dθ =∫_0 ^1 (∫_0 ^(π/2) ((r^2 sinθ)/(1+r^2 cos^2 θ))dθ)dr but ∫_0 ^(π/2) ((r^2 sinθ)/(1+r^2 cos^2 θ))=_(rcosθ=u) =∫_r ^0 ((−rdu)/(1+u^2 ))=r∫_0 ^r (du/(1+u^2 )) =rarctanr ⇒ A=∫_0 ^1 r arctan(r)dr =[(r^2 /2)arctanr]_0 ^1 −∫_0 ^1 (r^2 /2)(dr/(1+r^2 )) =(π/8)−(1/2)∫_0 ^1 ((1+r^2 −1)/(1+r^2 ))dr =(π/8)−(1/2) +(1/2)∫_0 ^1 (dr/(1+r^2 )) =(π/8)−(1/2)+(π/8)=(π/4)−(1/2)](https://www.tinkutara.com/question/Q170680.png)
$${A}=\int\int_{{D}} \frac{{y}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dx}\:{dy} \\ $$$${we}\:{do}\:{the}\:{changement}\:{x}={arcos}\theta \\ $$$${et}\:{y}={arsin}\theta\:\Rightarrow \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} \leqslant{a}^{\mathrm{2}} \Rightarrow{a}^{\mathrm{2}} {r}^{\mathrm{2}} \leqslant{a}^{\mathrm{2}} \Rightarrow\mathrm{0}\leqslant{r}\leqslant\mathrm{1} \\ $$$${x}\geqslant\mathrm{0}\:{and}\:{y}\geqslant\mathrm{0}\:\Rightarrow\mathrm{0}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow{A}=\int\int_{{o}\leqslant{r}\leqslant\mathrm{1}\:{and}\:{o}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}}} \:\:\frac{{arsin}\theta}{{a}^{\mathrm{2}} {r}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta+{a}^{\mathrm{2}} }{a}^{\mathrm{2}} {rdrd}\theta \\ $$$$={a}\int\int_{{o}\leqslant{r}\leqslant\mathrm{1}\:{and}\:\mathrm{0}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}}} \:\:\frac{{r}^{\mathrm{2}} {sin}\theta}{\mathrm{1}+{r}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta}{dr}\:{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{r}^{\mathrm{2}} {sin}\theta}{\mathrm{1}+{r}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta}{d}\theta\right){dr} \\ $$$${but}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{r}^{\mathrm{2}} {sin}\theta}{\mathrm{1}+{r}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta}=_{{rcos}\theta={u}} \\ $$$$=\int_{{r}} ^{\mathrm{0}} \frac{−{rdu}}{\mathrm{1}+{u}^{\mathrm{2}} }={r}\int_{\mathrm{0}} ^{{r}} \frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$={rarctanr}\:\Rightarrow \\ $$$${A}=\int_{\mathrm{0}} ^{\mathrm{1}} {r}\:{arctan}\left({r}\right){dr} \\ $$$$=\left[\frac{{r}^{\mathrm{2}} }{\mathrm{2}}{arctanr}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{r}^{\mathrm{2}} }{\mathrm{2}}\frac{{dr}}{\mathrm{1}+{r}^{\mathrm{2}} } \\ $$$$=\frac{\pi}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}+{r}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+{r}^{\mathrm{2}} }{dr} \\ $$$$=\frac{\pi}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dr}}{\mathrm{1}+{r}^{\mathrm{2}} } \\ $$$$=\frac{\pi}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\pi}{\mathrm{8}}=\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Mathspace last updated on 29/May/22

$${A}=\left(\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}\right){a} \\ $$
Answered by Mathspace last updated on 29/May/22
![C=∫∫∫_V xy dxdy dz we do the changement x=rcosθ y=rsinθ ⇒C=∫_0 ^1 (∫∫_w xydxdy)dz x^2 +y^2 ≤z^2 ⇒o≤r≤z ⇒ ∫∫_w xy dx dy=∫∫_(o≤r≤zand o≤θ≤2π) (rcosθ)(rsinθ)r drdθ =∫_0 ^z r^3 dr ∫_0 ^(2π) cosθsinθ =(z^4 /8)∫_0 ^(2π) sin(2θ)dθ =(z^4 /8)[−(1/2)cos(2θ)]_0 ^(2π) =0⇒C=0](https://www.tinkutara.com/question/Q170682.png)
$${C}=\int\int\int_{{V}} {xy}\:{dxdy}\:{dz} \\ $$$${we}\:{do}\:{the}\:{changement}\:{x}={rcos}\theta \\ $$$${y}={rsin}\theta\:\Rightarrow{C}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\int\int_{{w}} {xydxdy}\right){dz} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} \leqslant{z}^{\mathrm{2}} \Rightarrow{o}\leqslant{r}\leqslant{z}\:\Rightarrow \\ $$$$\int\int_{{w}} {xy}\:{dx}\:{dy}=\int\int_{{o}\leqslant{r}\leqslant{zand}\:{o}\leqslant\theta\leqslant\mathrm{2}\pi} \left({rcos}\theta\right)\left({rsin}\theta\right){r}\:{drd}\theta \\ $$$$=\int_{\mathrm{0}} ^{{z}} {r}^{\mathrm{3}} {dr}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} {cos}\theta{sin}\theta \\ $$$$=\frac{{z}^{\mathrm{4}} }{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{2}\pi} {sin}\left(\mathrm{2}\theta\right){d}\theta \\ $$$$=\frac{{z}^{\mathrm{4}} }{\mathrm{8}}\left[−\frac{\mathrm{1}}{\mathrm{2}}{cos}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\mathrm{2}\pi} =\mathrm{0}\Rightarrow{C}=\mathrm{0} \\ $$
