Question Number 170673 by solomonwells last updated on 28/May/22

Commented by cortano1 last updated on 29/May/22
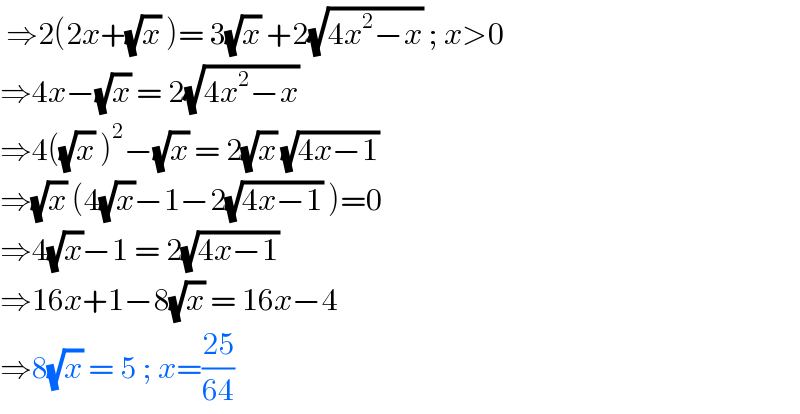
$$\:\Rightarrow\mathrm{2}\left(\mathrm{2}{x}+\sqrt{{x}}\:\right)=\:\mathrm{3}\sqrt{{x}}\:+\mathrm{2}\sqrt{\mathrm{4}{x}^{\mathrm{2}} −{x}}\:;\:{x}>\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}{x}−\sqrt{{x}}\:=\:\mathrm{2}\sqrt{\mathrm{4}{x}^{\mathrm{2}} −{x}} \\ $$$$\Rightarrow\mathrm{4}\left(\sqrt{{x}}\:\right)^{\mathrm{2}} −\sqrt{{x}}\:=\:\mathrm{2}\sqrt{{x}}\:\sqrt{\mathrm{4}{x}−\mathrm{1}} \\ $$$$\Rightarrow\sqrt{{x}}\:\left(\mathrm{4}\sqrt{{x}}−\mathrm{1}−\mathrm{2}\sqrt{\mathrm{4}{x}−\mathrm{1}}\:\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{4}\sqrt{{x}}−\mathrm{1}\:=\:\mathrm{2}\sqrt{\mathrm{4}{x}−\mathrm{1}} \\ $$$$\Rightarrow\mathrm{16}{x}+\mathrm{1}−\mathrm{8}\sqrt{{x}}\:=\:\mathrm{16}{x}−\mathrm{4} \\ $$$$\Rightarrow\mathrm{8}\sqrt{{x}}\:=\:\mathrm{5}\:;\:{x}=\frac{\mathrm{25}}{\mathrm{64}}\: \\ $$
Commented by solomonwells last updated on 29/May/22
$$\mathrm{thanks}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir} \\ $$
