Question-170722

Question Number 170722 by Sotoberry last updated on 29/May/22

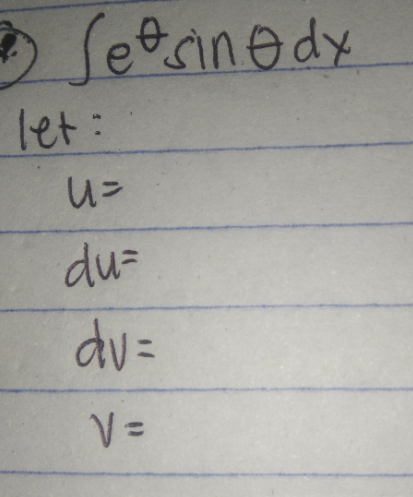
Answered by MikeH last updated on 29/May/22

u =sin θ du = cos θ dθ dv = e^θ dθ v = e^θ ⇒ ∫e^θ sin θ dθ = [e^θ sin θ]−∫e^θ cos θ dθ ∫e^θ cos θ dθ = [−e^θ cos θ] + ∫e^θ sin θdθ ⇒ 2∫e^θ sin θ dθ = e^θ sin θ −e^θ cos θ ⇒ ∫e^θ sin θdθ = (e^θ /2)(sin θ −cos θ)

$${u}\:=\mathrm{sin}\:\theta \\ $$$${du}\:=\:\mathrm{cos}\:\theta\:{d}\theta \\ $$$${dv}\:=\:{e}^{\theta} {d}\theta \\ $$$${v}\:=\:{e}^{\theta} \\ $$$$\Rightarrow\:\int{e}^{\theta} \mathrm{sin}\:\theta\:{d}\theta\:=\:\left[{e}^{\theta} \mathrm{sin}\:\theta\right]−\int{e}^{\theta} \mathrm{cos}\:\theta\:{d}\theta \\ $$$$\int{e}^{\theta} \:\mathrm{cos}\:\theta\:{d}\theta\:=\:\left[−{e}^{\theta} \mathrm{cos}\:\theta\right]\:+\:\int{e}^{\theta} \mathrm{sin}\:\theta{d}\theta \\ $$$$\Rightarrow\:\mathrm{2}\int{e}^{\theta} \:\mathrm{sin}\:\theta\:{d}\theta\:=\:{e}^{\theta} \mathrm{sin}\:\theta\:−{e}^{\theta} \mathrm{cos}\:\theta \\ $$$$\Rightarrow\:\int{e}^{\theta} \mathrm{sin}\:\theta{d}\theta\:=\:\frac{{e}^{\theta} }{\mathrm{2}}\left(\mathrm{sin}\:\theta\:−\mathrm{cos}\:\theta\right) \\ $$

Answered by floor(10²Eta[1]) last updated on 29/May/22

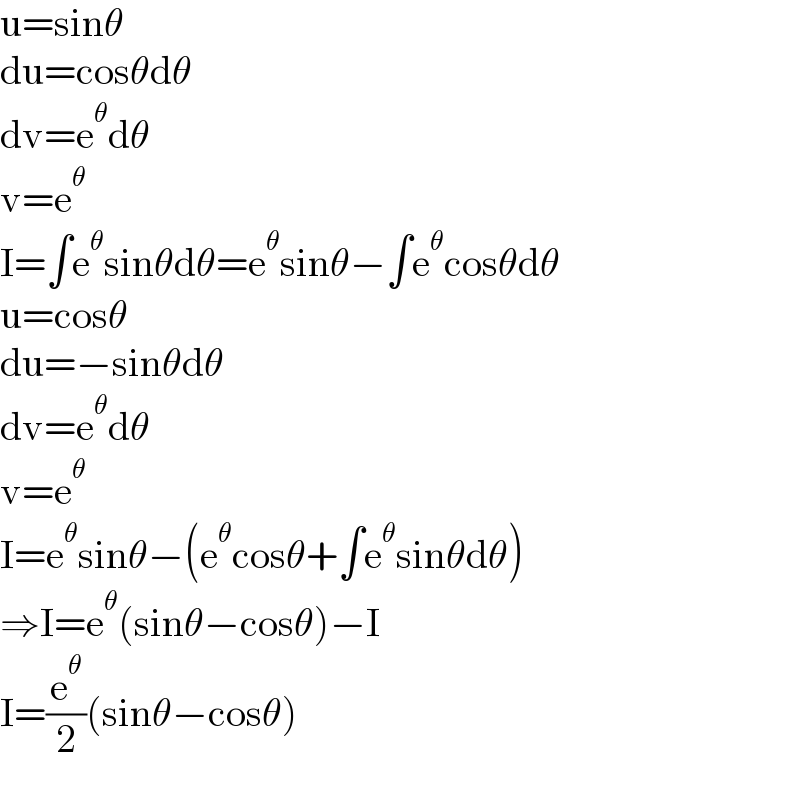
u=sinθ du=cosθdθ dv=e^θ dθ v=e^θ I=∫e^θ sinθdθ=e^θ sinθ−∫e^θ cosθdθ u=cosθ du=−sinθdθ dv=e^θ dθ v=e^θ I=e^θ sinθ−(e^θ cosθ+∫e^θ sinθdθ) ⇒I=e^θ (sinθ−cosθ)−I I=(e^θ /2)(sinθ−cosθ)

$$\mathrm{u}=\mathrm{sin}\theta \\ $$$$\mathrm{du}=\mathrm{cos}\theta\mathrm{d}\theta \\ $$$$\mathrm{dv}=\mathrm{e}^{\theta} \mathrm{d}\theta \\ $$$$\mathrm{v}=\mathrm{e}^{\theta} \\ $$$$\mathrm{I}=\int\mathrm{e}^{\theta} \mathrm{sin}\theta\mathrm{d}\theta=\mathrm{e}^{\theta} \mathrm{sin}\theta−\int\mathrm{e}^{\theta} \mathrm{cos}\theta\mathrm{d}\theta \\ $$$$\mathrm{u}=\mathrm{cos}\theta \\ $$$$\mathrm{du}=−\mathrm{sin}\theta\mathrm{d}\theta \\ $$$$\mathrm{dv}=\mathrm{e}^{\theta} \mathrm{d}\theta \\ $$$$\mathrm{v}=\mathrm{e}^{\theta} \\ $$$$\mathrm{I}=\mathrm{e}^{\theta} \mathrm{sin}\theta−\left(\mathrm{e}^{\theta} \mathrm{cos}\theta+\int\mathrm{e}^{\theta} \mathrm{sin}\theta\mathrm{d}\theta\right) \\ $$$$\Rightarrow\mathrm{I}=\mathrm{e}^{\theta} \left(\mathrm{sin}\theta−\mathrm{cos}\theta\right)−\mathrm{I} \\ $$$$\mathrm{I}=\frac{\mathrm{e}^{\theta} }{\mathrm{2}}\left(\mathrm{sin}\theta−\mathrm{cos}\theta\right) \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply