Question Number 170725 by Sotoberry last updated on 29/May/22

Answered by FelipeLz last updated on 30/May/22
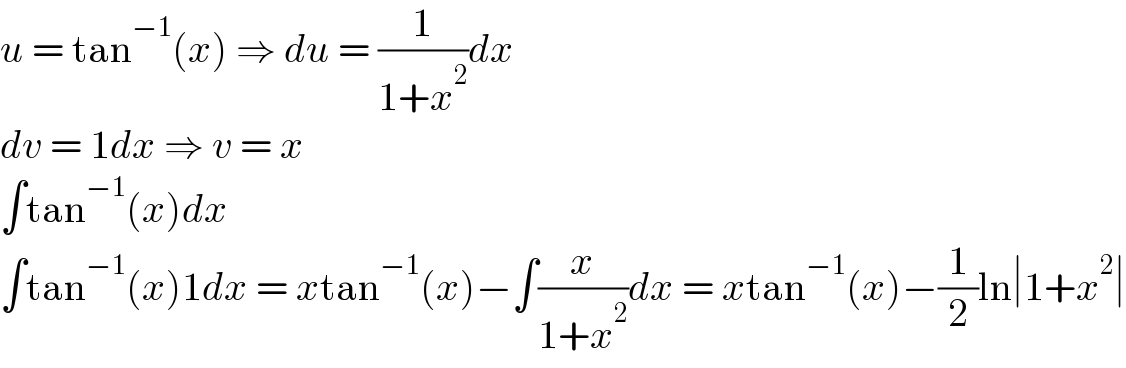
$${u}\:=\:\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\:\Rightarrow\:{du}\:=\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${dv}\:=\:\mathrm{1}{dx}\:\Rightarrow\:{v}\:=\:{x} \\ $$$$\int\mathrm{tan}^{−\mathrm{1}} \left({x}\right){dx} \\ $$$$\int\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\mathrm{1}{dx}\:=\:{x}\mathrm{tan}^{−\mathrm{1}} \left({x}\right)−\int\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:=\:{x}\mathrm{tan}^{−\mathrm{1}} \left({x}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{1}+{x}^{\mathrm{2}} \mid \\ $$
