Question-170729

Question Number 170729 by solomonwells last updated on 30/May/22

Commented by phamkhanhhuong last updated on 30/May/22

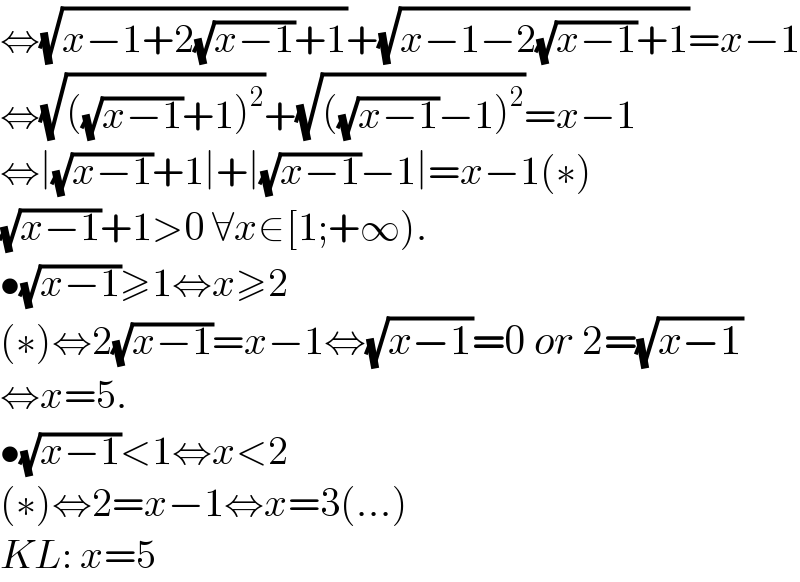
⇔(√(x−1+2(√(x−1))+1))+(√(x−1−2(√(x−1))+1))=x−1 ⇔(√(((√(x−1))+1)^2 ))+(√(((√(x−1))−1)^2 ))=x−1 ⇔∣(√(x−1))+1∣+∣(√(x−1))−1∣=x−1(∗) (√(x−1))+1>0 ∀x∈[1;+∞). •(√(x−1))≥1⇔x≥2 (∗)⇔2(√(x−1))=x−1⇔(√(x−1))=0 or 2=(√(x−1)) ⇔x=5. •(√(x−1))<1⇔x<2 (∗)⇔2=x−1⇔x=3(...) KL: x=5

$$\Leftrightarrow\sqrt{{x}−\mathrm{1}+\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{1}}+\sqrt{{x}−\mathrm{1}−\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{1}}={x}−\mathrm{1} \\ $$$$\Leftrightarrow\sqrt{\left(\sqrt{{x}−\mathrm{1}}+\mathrm{1}\right)^{\mathrm{2}} }+\sqrt{\left(\sqrt{{x}−\mathrm{1}}−\mathrm{1}\right)^{\mathrm{2}} }={x}−\mathrm{1} \\ $$$$\Leftrightarrow\mid\sqrt{{x}−\mathrm{1}}+\mathrm{1}\mid+\mid\sqrt{{x}−\mathrm{1}}−\mathrm{1}\mid={x}−\mathrm{1}\left(\ast\right) \\ $$$$\sqrt{{x}−\mathrm{1}}+\mathrm{1}>\mathrm{0}\:\forall{x}\in\left[\mathrm{1};+\infty\right). \\ $$$$\bullet\sqrt{{x}−\mathrm{1}}\geqslant\mathrm{1}\Leftrightarrow{x}\geqslant\mathrm{2} \\ $$$$\left(\ast\right)\Leftrightarrow\mathrm{2}\sqrt{{x}−\mathrm{1}}={x}−\mathrm{1}\Leftrightarrow\sqrt{{x}−\mathrm{1}}=\mathrm{0}\:{or}\:\mathrm{2}=\sqrt{{x}−\mathrm{1}} \\ $$$$\Leftrightarrow{x}=\mathrm{5}. \\ $$$$\bullet\sqrt{{x}−\mathrm{1}}<\mathrm{1}\Leftrightarrow{x}<\mathrm{2} \\ $$$$\left(\ast\right)\Leftrightarrow\mathrm{2}={x}−\mathrm{1}\Leftrightarrow{x}=\mathrm{3}\left(…\right) \\ $$$${KL}:\:{x}=\mathrm{5} \\ $$

Commented by Rasheed.Sindhi last updated on 30/May/22

$$\Cap\overset{\bullet} {\shortparallel}\Subset\overset{ } {\in}! \\ $$

Answered by MJS_new last updated on 30/May/22

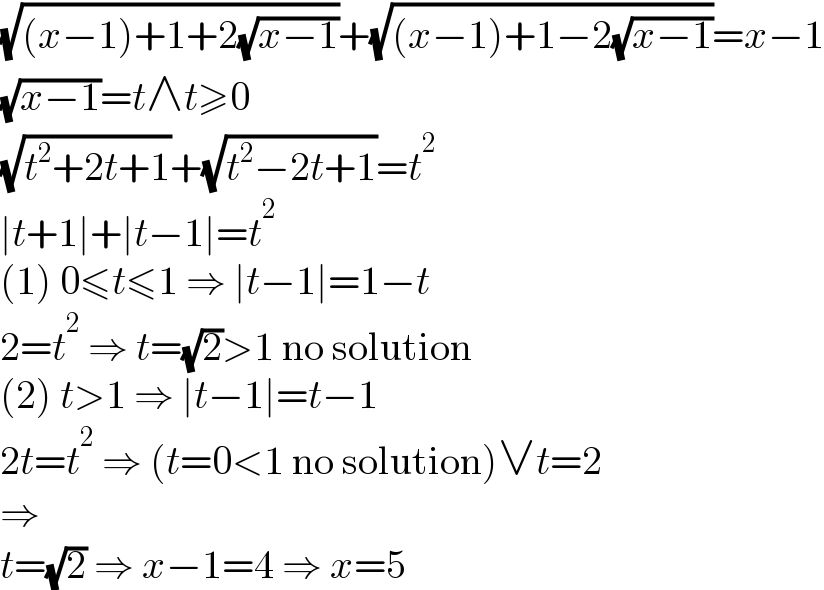
(√((x−1)+1+2(√(x−1))))+(√((x−1)+1−2(√(x−1))))=x−1 (√(x−1))=t∧t≥0 (√(t^2 +2t+1))+(√(t^2 −2t+1))=t^2 ∣t+1∣+∣t−1∣=t^2 (1) 0≤t≤1 ⇒ ∣t−1∣=1−t 2=t^2 ⇒ t=(√2)>1 no solution (2) t>1 ⇒ ∣t−1∣=t−1 2t=t^2 ⇒ (t=0<1 no solution)∨t=2 ⇒ t=(√2) ⇒ x−1=4 ⇒ x=5

$$\sqrt{\left({x}−\mathrm{1}\right)+\mathrm{1}+\mathrm{2}\sqrt{{x}−\mathrm{1}}}+\sqrt{\left({x}−\mathrm{1}\right)+\mathrm{1}−\mathrm{2}\sqrt{{x}−\mathrm{1}}}={x}−\mathrm{1} \\ $$$$\sqrt{{x}−\mathrm{1}}={t}\wedge{t}\geqslant\mathrm{0} \\ $$$$\sqrt{{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}}+\sqrt{{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}}={t}^{\mathrm{2}} \\ $$$$\mid{t}+\mathrm{1}\mid+\mid{t}−\mathrm{1}\mid={t}^{\mathrm{2}} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{0}\leqslant{t}\leqslant\mathrm{1}\:\Rightarrow\:\mid{t}−\mathrm{1}\mid=\mathrm{1}−{t} \\ $$$$\mathrm{2}={t}^{\mathrm{2}} \:\Rightarrow\:{t}=\sqrt{\mathrm{2}}>\mathrm{1}\:\mathrm{no}\:\mathrm{solution} \\ $$$$\left(\mathrm{2}\right)\:{t}>\mathrm{1}\:\Rightarrow\:\mid{t}−\mathrm{1}\mid={t}−\mathrm{1} \\ $$$$\mathrm{2}{t}={t}^{\mathrm{2}} \:\Rightarrow\:\left({t}=\mathrm{0}<\mathrm{1}\:\mathrm{no}\:\mathrm{solution}\right)\vee{t}=\mathrm{2} \\ $$$$\Rightarrow \\ $$$${t}=\sqrt{\mathrm{2}}\:\Rightarrow\:{x}−\mathrm{1}=\mathrm{4}\:\Rightarrow\:{x}=\mathrm{5} \\ $$

Answered by som(math1967) last updated on 30/May/22

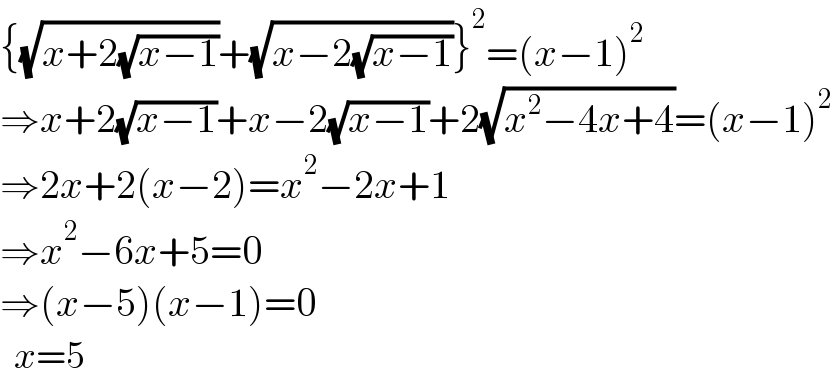
{(√(x+2(√(x−1))))+(√(x−2(√(x−1))))}^2 =(x−1)^2 ⇒x+2(√(x−1))+x−2(√(x−1))+2(√(x^2 −4x+4))=(x−1)^2 ⇒2x+2(x−2)=x^2 −2x+1 ⇒x^2 −6x+5=0 ⇒(x−5)(x−1)=0 x=5

$$\left\{\sqrt{{x}+\mathrm{2}\sqrt{{x}−\mathrm{1}}}+\sqrt{{x}−\mathrm{2}\sqrt{{x}−\mathrm{1}}}\right\}^{\mathrm{2}} =\left({x}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{x}+\mathrm{2}\sqrt{{x}−\mathrm{1}}+{x}−\mathrm{2}\sqrt{{x}−\mathrm{1}}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}}=\left({x}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{x}+\mathrm{2}\left({x}−\mathrm{2}\right)={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{5}=\mathrm{0} \\ $$$$\Rightarrow\left({x}−\mathrm{5}\right)\left({x}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\:{x}=\mathrm{5} \\ $$

Commented by Tawa11 last updated on 30/May/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Answered by Rasheed.Sindhi last updated on 30/May/22

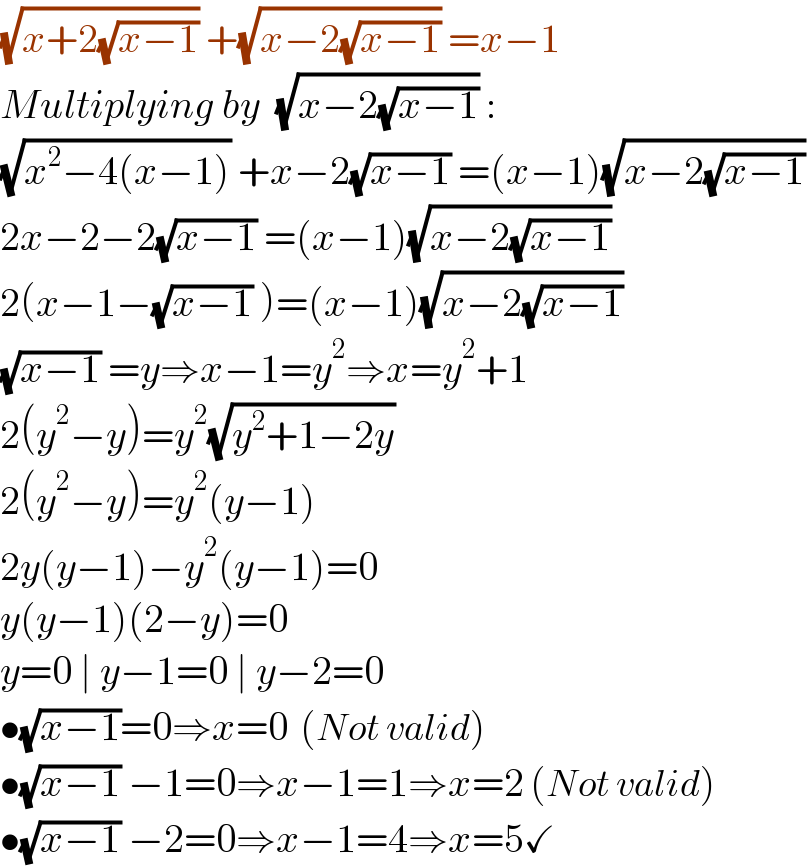
(√(x+2(√(x−1)))) +(√(x−2(√(x−1)))) =x−1 Multiplying by (√(x−2(√(x−1)))) : (√(x^2 −4(x−1))) +x−2(√(x−1)) =(x−1)(√(x−2(√(x−1)))) 2x−2−2(√(x−1)) =(x−1)(√(x−2(√(x−1)))) 2(x−1−(√(x−1)) )=(x−1)(√(x−2(√(x−1)))) (√(x−1)) =y⇒x−1=y^2 ⇒x=y^2 +1 2(y^2 −y)=y^2 (√(y^2 +1−2y)) 2(y^2 −y)=y^2 (y−1) 2y(y−1)−y^2 (y−1)=0 y(y−1)(2−y)=0 y=0 ∣ y−1=0 ∣ y−2=0 •(√(x−1))=0⇒x=0 (Not valid) •(√(x−1)) −1=0⇒x−1=1⇒x=2 (Not valid) •(√(x−1)) −2=0⇒x−1=4⇒x=5✓

$$\sqrt{{x}+\mathrm{2}\sqrt{{x}−\mathrm{1}}}\:+\sqrt{{x}−\mathrm{2}\sqrt{{x}−\mathrm{1}}}\:={x}−\mathrm{1} \\ $$$${Multiplying}\:{by}\:\:\sqrt{{x}−\mathrm{2}\sqrt{{x}−\mathrm{1}}}\:: \\ $$$$\sqrt{{x}^{\mathrm{2}} −\mathrm{4}\left({x}−\mathrm{1}\right)}\:+{x}−\mathrm{2}\sqrt{{x}−\mathrm{1}}\:=\left({x}−\mathrm{1}\right)\sqrt{{x}−\mathrm{2}\sqrt{{x}−\mathrm{1}}}\: \\ $$$$\mathrm{2}{x}−\mathrm{2}−\mathrm{2}\sqrt{{x}−\mathrm{1}}\:=\left({x}−\mathrm{1}\right)\sqrt{{x}−\mathrm{2}\sqrt{{x}−\mathrm{1}}}\: \\ $$$$\mathrm{2}\left({x}−\mathrm{1}−\sqrt{{x}−\mathrm{1}}\:\right)=\left({x}−\mathrm{1}\right)\sqrt{{x}−\mathrm{2}\sqrt{{x}−\mathrm{1}}}\: \\ $$$$\sqrt{{x}−\mathrm{1}}\:={y}\Rightarrow{x}−\mathrm{1}={y}^{\mathrm{2}} \Rightarrow{x}={y}^{\mathrm{2}} +\mathrm{1} \\ $$$$\mathrm{2}\left({y}^{\mathrm{2}} −{y}\right)={y}^{\mathrm{2}} \sqrt{{y}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{y}} \\ $$$$\mathrm{2}\left({y}^{\mathrm{2}} −{y}\right)={y}^{\mathrm{2}} \left({y}−\mathrm{1}\right) \\ $$$$\mathrm{2}{y}\left({y}−\mathrm{1}\right)−{y}^{\mathrm{2}} \left({y}−\mathrm{1}\right)=\mathrm{0} \\ $$$${y}\left({y}−\mathrm{1}\right)\left(\mathrm{2}−{y}\right)=\mathrm{0} \\ $$$${y}=\mathrm{0}\:\mid\:{y}−\mathrm{1}=\mathrm{0}\:\mid\:{y}−\mathrm{2}=\mathrm{0} \\ $$$$\bullet\sqrt{{x}−\mathrm{1}}=\mathrm{0}\Rightarrow{x}=\mathrm{0}\:\:\left({Not}\:{valid}\right) \\ $$$$\bullet\sqrt{{x}−\mathrm{1}}\:−\mathrm{1}=\mathrm{0}\Rightarrow{x}−\mathrm{1}=\mathrm{1}\Rightarrow{x}=\mathrm{2}\:\left({Not}\:{valid}\right) \\ $$$$\bullet\sqrt{{x}−\mathrm{1}}\:−\mathrm{2}=\mathrm{0}\Rightarrow{x}−\mathrm{1}=\mathrm{4}\Rightarrow{x}=\mathrm{5}\checkmark \\ $$

Commented by Tawa11 last updated on 30/May/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply