Question Number 170738 by Tawa11 last updated on 30/May/22

Commented by Tawa11 last updated on 30/May/22

$$\mathrm{How}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the}\:\mathrm{second}\:\mathrm{step}\:\mathrm{please}???? \\ $$$$\mathrm{S}\:\:\:=\:\:\:\frac{\mathrm{1}}{\mathrm{8}}\underset{\mathrm{n}\:=\:\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{3}}{\left(\mathrm{3n}\:+\:\mathrm{1}\right)\left(\mathrm{3n}\:+\:\mathrm{2}\right)}\:\:−\:\:\frac{\mathrm{5}}{\left(\mathrm{3n}\:+\:\mathrm{2}\right)\left(\mathrm{3n}\:+\:\mathrm{3}\right)}\:\:+\:\:\frac{\mathrm{2}}{\left(\mathrm{3n}\:+\:\mathrm{3}\right)\left(\mathrm{3n}\:+\:\mathrm{1}\right)} \\ $$$$\mathrm{From}\:\mathrm{the}\:\mathrm{question}\:… \\ $$
Commented by mr W last updated on 30/May/22
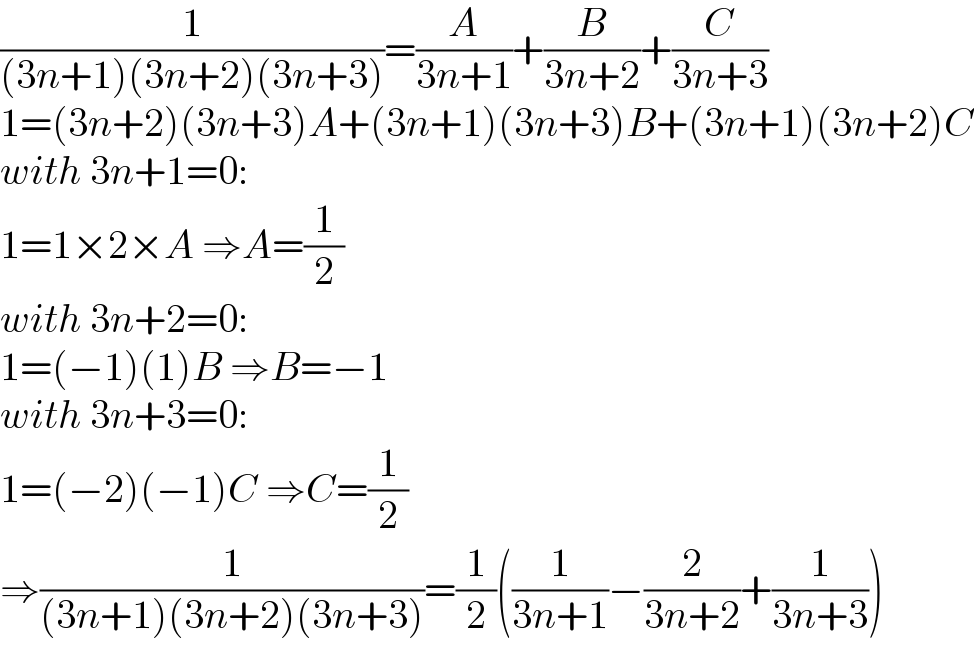
$$\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)\left(\mathrm{3}{n}+\mathrm{3}\right)}=\frac{{A}}{\mathrm{3}{n}+\mathrm{1}}+\frac{{B}}{\mathrm{3}{n}+\mathrm{2}}+\frac{{C}}{\mathrm{3}{n}+\mathrm{3}} \\ $$$$\mathrm{1}=\left(\mathrm{3}{n}+\mathrm{2}\right)\left(\mathrm{3}{n}+\mathrm{3}\right){A}+\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{3}\right){B}+\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right){C} \\ $$$${with}\:\mathrm{3}{n}+\mathrm{1}=\mathrm{0}: \\ $$$$\mathrm{1}=\mathrm{1}×\mathrm{2}×{A}\:\Rightarrow{A}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${with}\:\mathrm{3}{n}+\mathrm{2}=\mathrm{0}: \\ $$$$\mathrm{1}=\left(−\mathrm{1}\right)\left(\mathrm{1}\right){B}\:\Rightarrow{B}=−\mathrm{1} \\ $$$${with}\:\mathrm{3}{n}+\mathrm{3}=\mathrm{0}: \\ $$$$\mathrm{1}=\left(−\mathrm{2}\right)\left(−\mathrm{1}\right){C}\:\Rightarrow{C}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)\left(\mathrm{3}{n}+\mathrm{3}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{3}{n}+\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{3}{n}+\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}{n}+\mathrm{3}}\right) \\ $$
Commented by Tawa11 last updated on 30/May/22
$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir}. \\ $$
Commented by Tawa11 last updated on 30/May/22
$$\mathrm{I}\:\mathrm{understand}\:\mathrm{this}\:\mathrm{sir} \\ $$
Commented by Tawa11 last updated on 30/May/22

Commented by Tawa11 last updated on 30/May/22
$$\mathrm{Is}\:\mathrm{that}\:\mathrm{particular}\:\mathrm{expression}\:\mathrm{I}\:\mathrm{want}. \\ $$
Commented by Tawa11 last updated on 30/May/22

$$\mathrm{The}\:\mathrm{second}\:\mathrm{step}\:… \\ $$
Commented by mr W last updated on 30/May/22
![(1/((3n+1)(3n+2)(3n+3)))=(A/((3n+1)(3n+2)))+(B/((3n+2)(3n+3)))+(C/((3n+3)(3n+1))) (1/((3n+1)(3n+2)(3n+3)))=((3n(A+B+C)+(3A+B+2C))/((3n+1)(3n+2)(3n+1))) ⇒A+B+C=0 ⇒3A+B+2C=1 ⇒2A+2B+2C+A−B=1 ⇒A−B=1 you may find infinite possibilities for A,B,C. for example as the step 2 in the solution did: A=(3/8), B=−(5/8), C=(2/8) A+B+C=((3−5+2)/8)=0 ✓ 3A+B+2C=((3×3−5+2×2)/8)=1 ✓ but this was arbitrarily done. so you don′t need to request yourself to get the same. certainly you can also take other values for A,B,C, because as i said there are infinite solutions. but you don′t need to take any special values for A,B,C in order to solve the problem. Σ_(n=0) ^∞ (1/((3n+1)(3n+2)(3n+3))) =Σ_(n=0) ^∞ [(A/((3n+1)(3n+2)))+(B/((3n+2)(3n+3)))+(C/((3n+3)(3n+1)))] =(1/9)Σ_(n=0) ^∞ [(A/((n+(1/3))(n+(2/3))))+(B/((n+(2/3))(n+1)))+(C/((n+1)(n+(1/3))))] =(1/9){((A[ψ((2/3))−ψ((1/3))])/((2/3)−(1/3)))+((B[ψ(1)−ψ((2/3))])/(1−(2/3)))+((C[ψ(1)−ψ((1/3))])/(1−(1/3)))} =(1/3){((A[ψ((2/3))−ψ((1/3))])/1)+((B[ψ(1)−ψ((2/3))])/1)+((C[ψ(1)−ψ((1/3))])/2)} =(1/6){2A[ψ((2/3))−ψ((1/3))]+2B[ψ(1)−ψ((2/3))]+C[ψ(1)−ψ((1/3))]} =(1/6){2Aψ((2/3))−2Aψ((1/3))+2Bψ(1)−2Bψ((2/3))+Cψ(1)−Cψ((1/3))} =(2/3){(2A−2B)ψ((2/3))−(2A+C)ψ((1/3))+(2B+C)ψ(1)} =(1/6){(2A−2B)(ψ((1/3))+(π/( (√3))))−(2A+C)ψ((1/3))+(2B+C)ψ(1)} =(1/6){2(A−B)(π/( (√3)))+(2B+C)(ψ(1)−ψ((1/3)))} =(1/6){2(A−B)(π/( (√3)))+(2B+C)((π/(2(√3)))+(3/2)ln 3)} =(((A−B))/4)((π/( (√3)))−ln 3) =(1/4)((π/( (√3)))−ln 3) ✓](https://www.tinkutara.com/question/Q170782.png)
$$\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)\left(\mathrm{3}{n}+\mathrm{3}\right)}=\frac{{A}}{\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)}+\frac{{B}}{\left(\mathrm{3}{n}+\mathrm{2}\right)\left(\mathrm{3}{n}+\mathrm{3}\right)}+\frac{{C}}{\left(\mathrm{3}{n}+\mathrm{3}\right)\left(\mathrm{3}{n}+\mathrm{1}\right)} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)\left(\mathrm{3}{n}+\mathrm{3}\right)}=\frac{\mathrm{3}{n}\left({A}+{B}+{C}\right)+\left(\mathrm{3}{A}+{B}+\mathrm{2}{C}\right)}{\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)\left(\mathrm{3}{n}+\mathrm{1}\right)} \\ $$$$\Rightarrow{A}+{B}+{C}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{3}{A}+{B}+\mathrm{2}{C}=\mathrm{1}\: \\ $$$$\Rightarrow\mathrm{2}{A}+\mathrm{2}{B}+\mathrm{2}{C}+{A}−{B}=\mathrm{1} \\ $$$$\Rightarrow{A}−{B}=\mathrm{1} \\ $$$${you}\:{may}\:{find}\:{infinite}\:{possibilities} \\ $$$${for}\:{A},{B},{C}.\:{for}\:{example}\:{as}\:{the}\:{step}\:\mathrm{2} \\ $$$${in}\:{the}\:{solution}\:{did}: \\ $$$${A}=\frac{\mathrm{3}}{\mathrm{8}},\:{B}=−\frac{\mathrm{5}}{\mathrm{8}},\:{C}=\frac{\mathrm{2}}{\mathrm{8}} \\ $$$${A}+{B}+{C}=\frac{\mathrm{3}−\mathrm{5}+\mathrm{2}}{\mathrm{8}}=\mathrm{0}\:\checkmark \\ $$$$\mathrm{3}{A}+{B}+\mathrm{2}{C}=\frac{\mathrm{3}×\mathrm{3}−\mathrm{5}+\mathrm{2}×\mathrm{2}}{\mathrm{8}}=\mathrm{1}\:\checkmark \\ $$$${but}\:{this}\:{was}\:{arbitrarily}\:{done}.\:{so}\:{you} \\ $$$${don}'{t}\:{need}\:{to}\:{request}\:{yourself}\:{to}\:{get} \\ $$$${the}\:{same}. \\ $$$${certainly}\:{you}\:{can}\:{also}\:{take}\:{other} \\ $$$${values}\:{for}\:{A},{B},{C},\:{because}\:{as}\:{i}\:{said}\: \\ $$$${there}\:{are}\:{infinite}\:{solutions}. \\ $$$${but}\:{you}\:{don}'{t}\:{need}\:{to}\:{take}\:{any}\:{special} \\ $$$${values}\:{for}\:{A},{B},{C}\:{in}\:{order}\:{to}\:{solve}\:{the} \\ $$$${problem}. \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)\left(\mathrm{3}{n}+\mathrm{3}\right)} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{{A}}{\left(\mathrm{3}{n}+\mathrm{1}\right)\left(\mathrm{3}{n}+\mathrm{2}\right)}+\frac{{B}}{\left(\mathrm{3}{n}+\mathrm{2}\right)\left(\mathrm{3}{n}+\mathrm{3}\right)}+\frac{{C}}{\left(\mathrm{3}{n}+\mathrm{3}\right)\left(\mathrm{3}{n}+\mathrm{1}\right)}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{{A}}{\left({n}+\frac{\mathrm{1}}{\mathrm{3}}\right)\left({n}+\frac{\mathrm{2}}{\mathrm{3}}\right)}+\frac{{B}}{\left({n}+\frac{\mathrm{2}}{\mathrm{3}}\right)\left({n}+\mathrm{1}\right)}+\frac{{C}}{\left({n}+\mathrm{1}\right)\left({n}+\frac{\mathrm{1}}{\mathrm{3}}\right)}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left\{\frac{{A}\left[\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right]}{\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}}+\frac{{B}\left[\psi\left(\mathrm{1}\right)−\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\right]}{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}}+\frac{{C}\left[\psi\left(\mathrm{1}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right]}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left\{\frac{{A}\left[\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right]}{\mathrm{1}}+\frac{{B}\left[\psi\left(\mathrm{1}\right)−\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\right]}{\mathrm{1}}+\frac{{C}\left[\psi\left(\mathrm{1}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right]}{\mathrm{2}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left\{\mathrm{2}{A}\left[\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right]+\mathrm{2}{B}\left[\psi\left(\mathrm{1}\right)−\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\right]+{C}\left[\psi\left(\mathrm{1}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right]\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left\{\mathrm{2}{A}\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\mathrm{2}{A}\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\mathrm{2}{B}\psi\left(\mathrm{1}\right)−\mathrm{2}{B}\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)+{C}\psi\left(\mathrm{1}\right)−{C}\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right\} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\left\{\left(\mathrm{2}{A}−\mathrm{2}{B}\right)\psi\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\left(\mathrm{2}{A}+{C}\right)\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\left(\mathrm{2}{B}+{C}\right)\psi\left(\mathrm{1}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left\{\left(\mathrm{2}{A}−\mathrm{2}{B}\right)\left(\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\frac{\pi}{\:\sqrt{\mathrm{3}}}\right)−\left(\mathrm{2}{A}+{C}\right)\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\left(\mathrm{2}{B}+{C}\right)\psi\left(\mathrm{1}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left\{\mathrm{2}\left({A}−{B}\right)\frac{\pi}{\:\sqrt{\mathrm{3}}}+\left(\mathrm{2}{B}+{C}\right)\left(\psi\left(\mathrm{1}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left\{\mathrm{2}\left({A}−{B}\right)\frac{\pi}{\:\sqrt{\mathrm{3}}}+\left(\mathrm{2}{B}+{C}\right)\left(\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\:\mathrm{3}\right)\right\} \\ $$$$=\frac{\left({A}−{B}\right)}{\mathrm{4}}\left(\frac{\pi}{\:\sqrt{\mathrm{3}}}−\mathrm{ln}\:\mathrm{3}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\pi}{\:\sqrt{\mathrm{3}}}−\mathrm{ln}\:\mathrm{3}\right)\:\checkmark \\ $$
Commented by Tawa11 last updated on 30/May/22
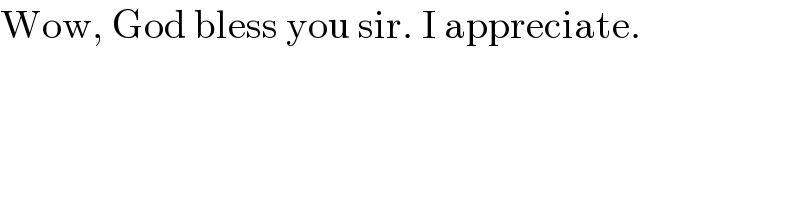
$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
