Question Number 170780 by Mastermind last updated on 30/May/22
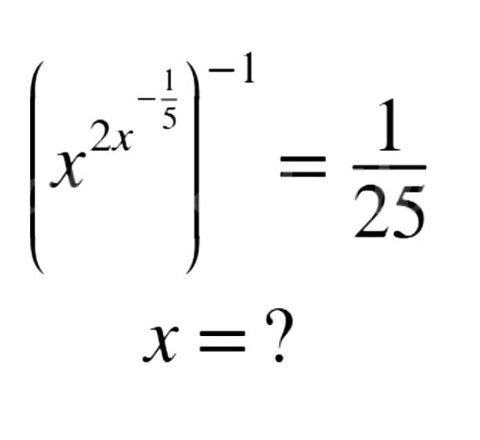
Answered by mr W last updated on 30/May/22
![x^(2x^(−(1/5)) ) =25 x^(2/x^(1/5) ) =5^2 x^2 =5^(2x^(1/5) ) (x^(1/5) )^2 =5^((2/5)x^(1/5) ) let t=x^(1/5) t^2 =(5^(t/5) )^2 t=5^(t/5) =e^((tln 5)/5) te^((−tln 5)/5) =1 (−((tln 5)/5))e^((−tln 5)/5) =−((ln 5)/5) −((tln 5)/5)=W(−((ln 5)/5)) t=−(5/(ln 5))W(−((ln 5)/5)) x^(1/5) =−(5/(ln 5))W(−((ln 5)/5)) ⇒x=[−(5/(ln 5))W(−((ln 5)/5))]^5 = { ((3125)),((17.124878)) :}](https://www.tinkutara.com/question/Q170788.png)
$${x}^{\mathrm{2}{x}^{−\frac{\mathrm{1}}{\mathrm{5}}} } =\mathrm{25} \\ $$$${x}^{\frac{\mathrm{2}}{{x}^{\frac{\mathrm{1}}{\mathrm{5}}} }} =\mathrm{5}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}{x}^{\frac{\mathrm{1}}{\mathrm{5}}} } \\ $$$$\left({x}^{\frac{\mathrm{1}}{\mathrm{5}}} \right)^{\mathrm{2}} =\mathrm{5}^{\frac{\mathrm{2}}{\mathrm{5}}{x}^{\frac{\mathrm{1}}{\mathrm{5}}} } \\ $$$${let}\:{t}={x}^{\frac{\mathrm{1}}{\mathrm{5}}} \\ $$$${t}^{\mathrm{2}} =\left(\mathrm{5}^{\frac{{t}}{\mathrm{5}}} \right)^{\mathrm{2}} \\ $$$${t}=\mathrm{5}^{\frac{{t}}{\mathrm{5}}} ={e}^{\frac{{t}\mathrm{ln}\:\mathrm{5}}{\mathrm{5}}} \\ $$$${te}^{\frac{−{t}\mathrm{ln}\:\mathrm{5}}{\mathrm{5}}} =\mathrm{1} \\ $$$$\left(−\frac{{t}\mathrm{ln}\:\mathrm{5}}{\mathrm{5}}\right){e}^{\frac{−{t}\mathrm{ln}\:\mathrm{5}}{\mathrm{5}}} =−\frac{\mathrm{ln}\:\mathrm{5}}{\mathrm{5}} \\ $$$$−\frac{{t}\mathrm{ln}\:\mathrm{5}}{\mathrm{5}}={W}\left(−\frac{\mathrm{ln}\:\mathrm{5}}{\mathrm{5}}\right) \\ $$$${t}=−\frac{\mathrm{5}}{\mathrm{ln}\:\mathrm{5}}{W}\left(−\frac{\mathrm{ln}\:\mathrm{5}}{\mathrm{5}}\right) \\ $$$${x}^{\frac{\mathrm{1}}{\mathrm{5}}} =−\frac{\mathrm{5}}{\mathrm{ln}\:\mathrm{5}}{W}\left(−\frac{\mathrm{ln}\:\mathrm{5}}{\mathrm{5}}\right) \\ $$$$\Rightarrow{x}=\left[−\frac{\mathrm{5}}{\mathrm{ln}\:\mathrm{5}}{W}\left(−\frac{\mathrm{ln}\:\mathrm{5}}{\mathrm{5}}\right)\right]^{\mathrm{5}} =\begin{cases}{\mathrm{3125}}\\{\mathrm{17}.\mathrm{124878}}\end{cases} \\ $$
Commented by Tawa11 last updated on 30/May/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Commented by Mastermind last updated on 31/May/22
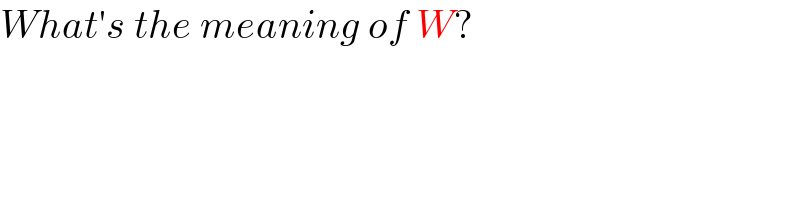
$${What}'{s}\:{the}\:{meaning}\:{of}\:{W}? \\ $$
Commented by mr W last updated on 31/May/22
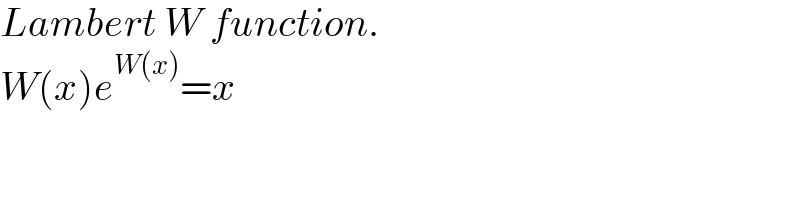
$${Lambert}\:{W}\:{function}. \\ $$$${W}\left({x}\right){e}^{{W}\left({x}\right)} ={x} \\ $$
Commented by Mastermind last updated on 31/May/22

$${Thanks} \\ $$
