Question Number 170796 by Beginner last updated on 31/May/22
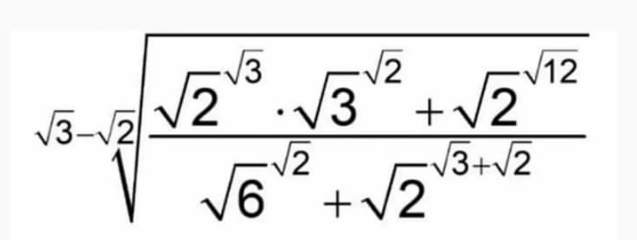
Answered by som(math1967) last updated on 31/May/22
![[((((√2))^(√3) {((√3))^(√2) +((√2))^(√3) })/(((√2))^(√2) {((√3))^(√2) +((√2))^(√3) }))]^(1/( (√3)−(√2))) ((√2))^(((√3)−(√2))/( (√3)−(√2))) =(√2) ans](https://www.tinkutara.com/question/Q170798.png)
$$\left[\frac{\left(\sqrt{\mathrm{2}}\right)^{\sqrt{\mathrm{3}}} \left\{\left(\sqrt{\mathrm{3}}\right)^{\sqrt{\mathrm{2}}} +\left(\sqrt{\mathrm{2}}\right)^{\sqrt{\mathrm{3}}} \right\}}{\left(\sqrt{\mathrm{2}}\right)^{\sqrt{\mathrm{2}}} \left\{\left(\sqrt{\mathrm{3}}\right)^{\sqrt{\mathrm{2}}} +\left(\sqrt{\mathrm{2}}\right)^{\sqrt{\mathrm{3}}} \right\}}\right]^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}}} \\ $$$$\left(\sqrt{\mathrm{2}}\right)^{\frac{\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}}} =\sqrt{\mathrm{2}}\:{ans} \\ $$$$ \\ $$
Answered by floor(10²Eta[1]) last updated on 31/May/22
![(√3)=b, (√2)=a [((a^b b^a +a^(2b) )/(a^a b^a +a^b a^a ))]^(1/(b−a)) =[((a^b (b^a +a^b ))/(a^a (b^a +a^b )))]^(1/(b−a)) =(a^(b−a) )^(1/(b−a)) =a=(√2)](https://www.tinkutara.com/question/Q170825.png)
$$\sqrt{\mathrm{3}}=\mathrm{b},\:\sqrt{\mathrm{2}}=\mathrm{a} \\ $$$$\left[\frac{\mathrm{a}^{\mathrm{b}} \mathrm{b}^{\mathrm{a}} +\mathrm{a}^{\mathrm{2b}} }{\mathrm{a}^{\mathrm{a}} \mathrm{b}^{\mathrm{a}} +\mathrm{a}^{\mathrm{b}} \mathrm{a}^{\mathrm{a}} }\right]^{\frac{\mathrm{1}}{\mathrm{b}−\mathrm{a}}} =\left[\frac{\mathrm{a}^{\mathrm{b}} \left(\mathrm{b}^{\mathrm{a}} +\mathrm{a}^{\mathrm{b}} \right)}{\mathrm{a}^{\mathrm{a}} \left(\mathrm{b}^{\mathrm{a}} +\mathrm{a}^{\mathrm{b}} \right)}\right]^{\frac{\mathrm{1}}{\mathrm{b}−\mathrm{a}}} =\left(\mathrm{a}^{\mathrm{b}−\mathrm{a}} \right)^{\frac{\mathrm{1}}{\mathrm{b}−\mathrm{a}}} =\mathrm{a}=\sqrt{\mathrm{2}} \\ $$
