Question Number 170832 by Shrinava last updated on 01/Jun/22

Commented by mr W last updated on 01/Jun/22
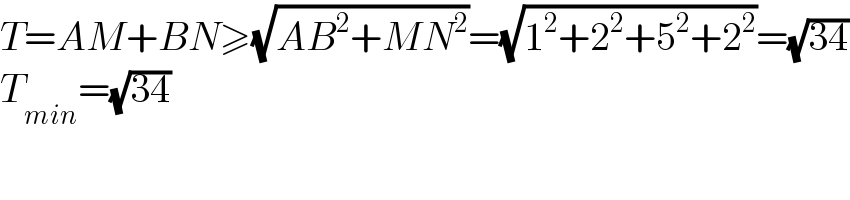
$${T}={AM}+{BN}\geqslant\sqrt{{AB}^{\mathrm{2}} +{MN}^{\mathrm{2}} }=\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }=\sqrt{\mathrm{34}} \\ $$$${T}_{{min}} =\sqrt{\mathrm{34}} \\ $$
Commented by Shrinava last updated on 01/Jun/22

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{dear}\:\mathrm{professor}, \\ $$$$\mathrm{can}\:\mathrm{you}\:\mathrm{explain}\:\mathrm{a}\:\mathrm{little}\:\mathrm{more}, \\ $$$$\mathrm{if}\:\mathrm{possible},\:\mathrm{please} \\ $$
Commented by mr W last updated on 02/Jun/22

Commented by mr W last updated on 01/Jun/22
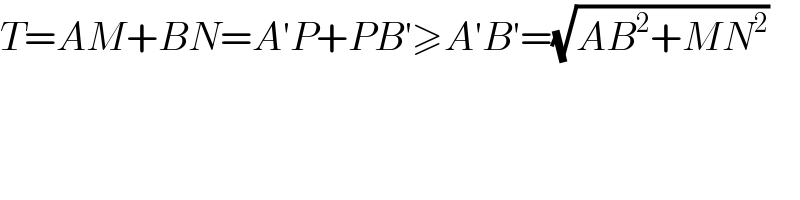
$${T}={AM}+{BN}={A}'{P}+{PB}'\geqslant{A}'{B}'=\sqrt{{AB}^{\mathrm{2}} +{MN}^{\mathrm{2}} } \\ $$
Commented by Shrinava last updated on 02/Jun/22
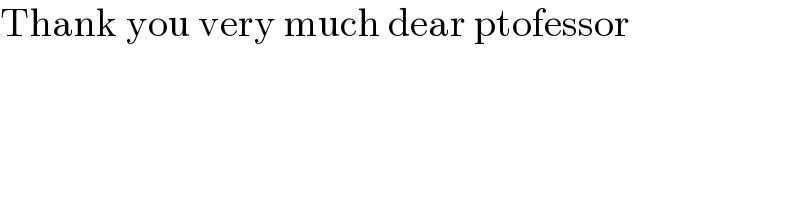
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{dear}\:\mathrm{ptofessor} \\ $$
Commented by mr W last updated on 04/Jun/22
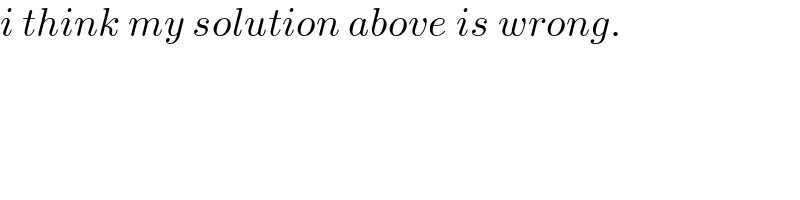
$${i}\:{think}\:{my}\:{solution}\:{above}\:{is}\:{wrong}. \\ $$
Commented by mr W last updated on 04/Jun/22

Commented by mr W last updated on 04/Jun/22
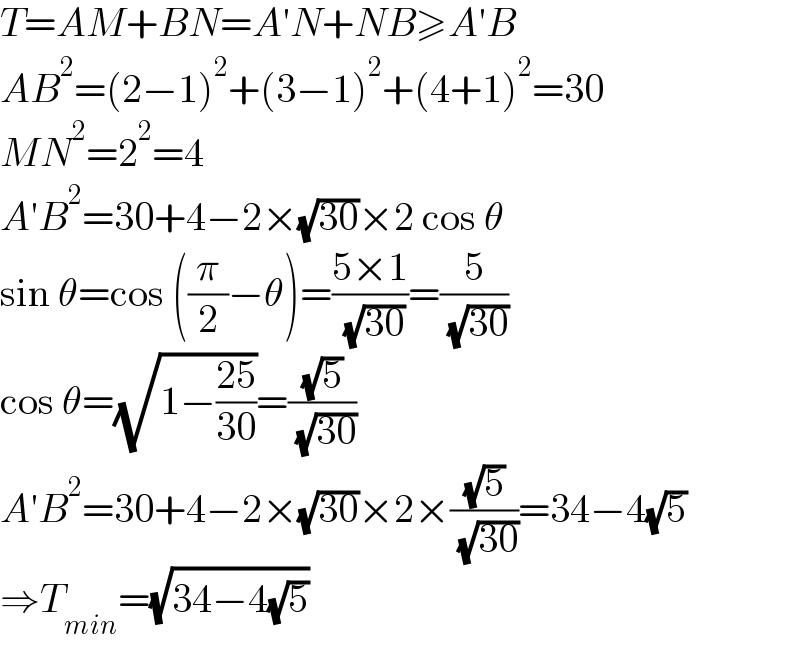
$${T}={AM}+{BN}={A}'{N}+{NB}\geqslant{A}'{B} \\ $$$${AB}^{\mathrm{2}} =\left(\mathrm{2}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{3}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{4}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{30} \\ $$$${MN}^{\mathrm{2}} =\mathrm{2}^{\mathrm{2}} =\mathrm{4} \\ $$$${A}'{B}^{\mathrm{2}} =\mathrm{30}+\mathrm{4}−\mathrm{2}×\sqrt{\mathrm{30}}×\mathrm{2}\:\mathrm{cos}\:\theta \\ $$$$\mathrm{sin}\:\theta=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−\theta\right)=\frac{\mathrm{5}×\mathrm{1}}{\:\sqrt{\mathrm{30}}}=\frac{\mathrm{5}}{\:\sqrt{\mathrm{30}}} \\ $$$$\mathrm{cos}\:\theta=\sqrt{\mathrm{1}−\frac{\mathrm{25}}{\mathrm{30}}}=\frac{\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{30}}} \\ $$$${A}'{B}^{\mathrm{2}} =\mathrm{30}+\mathrm{4}−\mathrm{2}×\sqrt{\mathrm{30}}×\mathrm{2}×\frac{\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{30}}}=\mathrm{34}−\mathrm{4}\sqrt{\mathrm{5}} \\ $$$$\Rightarrow{T}_{{min}} =\sqrt{\mathrm{34}−\mathrm{4}\sqrt{\mathrm{5}}} \\ $$
Commented by Shrinava last updated on 17/Jun/22

$$\mathrm{Perfect}-\mathrm{Amazing}\:\mathrm{Dear}\:\mathrm{Professor} \\ $$
