Question Number 170914 by mathlove last updated on 03/Jun/22

Commented by infinityaction last updated on 03/Jun/22
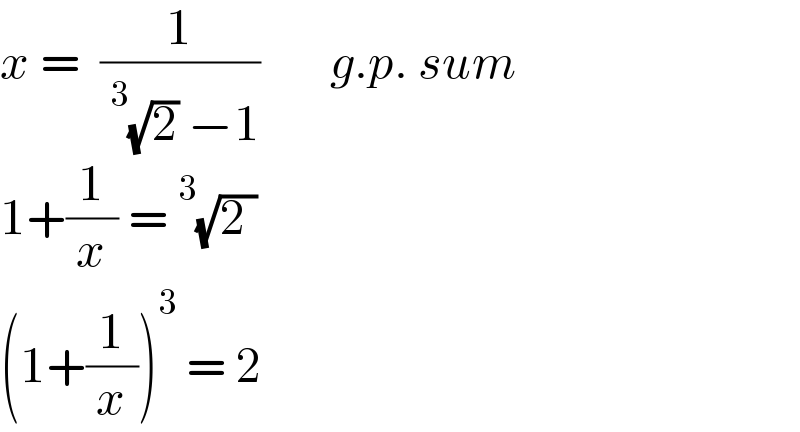
$${x}\:=\:\:\frac{\mathrm{1}}{\:^{\mathrm{3}} \sqrt{\mathrm{2}}\:−\mathrm{1}}\:\:\:\:\:\:\:{g}.{p}.\:{sum} \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{{x}}\:=\:^{\mathrm{3}} \sqrt{\mathrm{2}\:} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{3}} \:=\:\mathrm{2} \\ $$
Commented by cortano1 last updated on 04/Jun/22
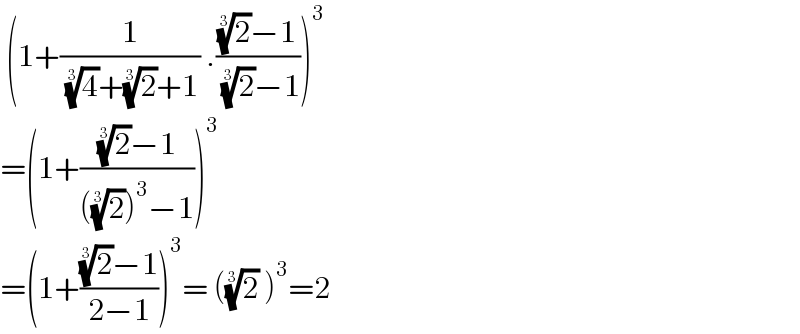
$$\:\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{4}}+\sqrt[{\mathrm{3}}]{\mathrm{2}}+\mathrm{1}}\:.\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}}\right)^{\mathrm{3}} \\ $$$$=\left(\mathrm{1}+\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}}{\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}\right)^{\mathrm{3}} −\mathrm{1}}\right)^{\mathrm{3}} \\ $$$$=\left(\mathrm{1}+\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}}−\mathrm{1}}{\mathrm{2}−\mathrm{1}}\right)^{\mathrm{3}} =\:\left(\sqrt[{\mathrm{3}}]{\mathrm{2}}\:\right)^{\mathrm{3}} =\mathrm{2} \\ $$
Commented by mathlove last updated on 04/Jun/22

$${tanks}\:{for}\:{all} \\ $$
Answered by mahdipoor last updated on 03/Jun/22
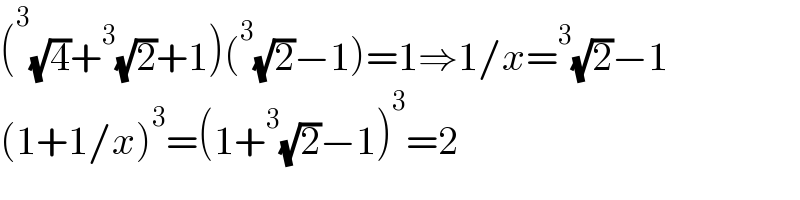
$$\left(^{\mathrm{3}} \sqrt{\mathrm{4}}+^{\mathrm{3}} \sqrt{\mathrm{2}}+\mathrm{1}\right)\left(^{\mathrm{3}} \sqrt{\mathrm{2}}−\mathrm{1}\right)=\mathrm{1}\Rightarrow\mathrm{1}/{x}=^{\mathrm{3}} \sqrt{\mathrm{2}}−\mathrm{1} \\ $$$$\left(\mathrm{1}+\mathrm{1}/{x}\right)^{\mathrm{3}} =\left(\mathrm{1}+^{\mathrm{3}} \sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{3}} =\mathrm{2} \\ $$
