Question Number 170968 by 281981 last updated on 05/Jun/22

Commented by mr W last updated on 05/Jun/22
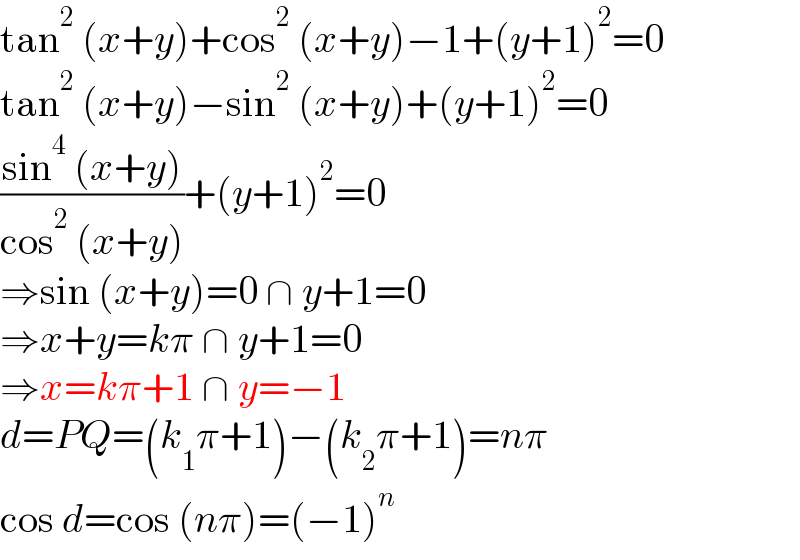
$$\mathrm{tan}^{\mathrm{2}} \:\left({x}+{y}\right)+\mathrm{cos}^{\mathrm{2}} \:\left({x}+{y}\right)−\mathrm{1}+\left({y}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{tan}^{\mathrm{2}} \:\left({x}+{y}\right)−\mathrm{sin}^{\mathrm{2}} \:\left({x}+{y}\right)+\left({y}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{\mathrm{sin}^{\mathrm{4}} \:\left({x}+{y}\right)}{\mathrm{cos}^{\mathrm{2}} \:\left({x}+{y}\right)}+\left({y}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\left({x}+{y}\right)=\mathrm{0}\:\cap\:{y}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}+{y}={k}\pi\:\cap\:{y}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}={k}\pi+\mathrm{1}\:\cap\:{y}=−\mathrm{1} \\ $$$${d}={PQ}=\left({k}_{\mathrm{1}} \pi+\mathrm{1}\right)−\left({k}_{\mathrm{2}} \pi+\mathrm{1}\right)={n}\pi \\ $$$$\mathrm{cos}\:{d}=\mathrm{cos}\:\left({n}\pi\right)=\left(−\mathrm{1}\right)^{{n}} \\ $$
Commented by 281981 last updated on 05/Jun/22

$$\boldsymbol{\mathrm{tnq}}\:\boldsymbol{\mathrm{sir}} \\ $$
