Question-171046

Question Number 171046 by Beginner last updated on 06/Jun/22

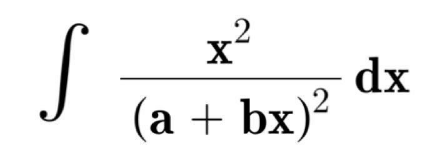
Answered by thfchristopher last updated on 07/Jun/22

Let u = a + b x

d u = b d x, x = \frac{u - a}{b}

∴ \int \frac{x^{2}}{{(a + b x)}^{2}} d x

= \frac{1}{b^{3}} \int \frac{{(u - a)}^{2}}{u^{2}} d u

= \frac{1}{b^{3}} \int \frac{u^{2} - 2 a u + a^{2}}{u^{2}} d u

= \frac{1}{b^{3}} (\int d u - 2 a \int \frac{1}{u} d u + a^{2} \int \frac{1}{u^{2}} d u)

= \frac{1}{b^{3}} (u - 2 a \ln u - \frac{a^{2}}{u}) + C

= \frac{1}{b^{3}} [(a + b x) + 2 a \ln (a + b x) - \frac{a^{2}}{(a + b x)}] + C

Answered by floor(10²Eta[1]) last updated on 06/Jun/22

I = \int {(\frac{x}{a + bx})}^{2} dx

x = (a + bx) q + r = bqx + aq + r

\Rightarrow bq = 1, aq + r = 0

\Rightarrow q = \frac{1}{b}, r = - \frac{a}{b}

I = \int {(\frac{1}{b} - \frac{a}{b (a + bx)})}^{2} dx

= \int (\frac{1}{b^{2}} - \frac{2 a}{b^{2} (a + bx)} + \frac{a^{2}}{b^{2} {(a + bx)}^{2}}) dx

= \frac{x}{b^{2}} - \frac{2 aln (a + bx)}{b^{3}} - \frac{a^{2}}{b^{3}} (\frac{1}{a + bx}) + C

[easily done by letting u = a + bx]