Question Number 171091 by pablo1234523 last updated on 07/Jun/22

Commented by pablo1234523 last updated on 07/Jun/22
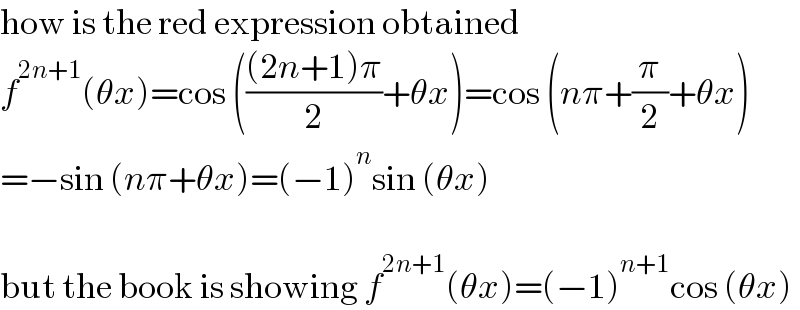
$$\mathrm{how}\:\mathrm{is}\:\mathrm{the}\:\mathrm{red}\:\mathrm{expression}\:\mathrm{obtained} \\ $$$${f}^{\mathrm{2}{n}+\mathrm{1}} \left(\theta{x}\right)=\mathrm{cos}\:\left(\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)\pi}{\mathrm{2}}+\theta{x}\right)=\mathrm{cos}\:\left({n}\pi+\frac{\pi}{\mathrm{2}}+\theta{x}\right) \\ $$$$=−\mathrm{sin}\:\left({n}\pi+\theta{x}\right)=\left(−\mathrm{1}\right)^{{n}} \mathrm{sin}\:\left(\theta{x}\right) \\ $$$$ \\ $$$$\mathrm{but}\:\mathrm{the}\:\mathrm{book}\:\mathrm{is}\:\mathrm{showing}\:{f}^{\mathrm{2}{n}+\mathrm{1}} \left(\theta{x}\right)=\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \mathrm{cos}\:\left(\theta{x}\right) \\ $$
Commented by pablo1234523 last updated on 07/Jun/22

$${please}\:{help} \\ $$
